Techniklexikon

integrable Modelle der Physik

Quantenmechanik, exakt lösbare Modelle, die in der theoretischen Physik in mehrfacher Hinsicht von Bedeutung sind. An ihnen lassen sich Näherungsverfahren oder Integrabilitätskriterien testen und allgemeine Mechanismen oder Relationen konkret realisieren. Ausserdem sind sie oft Ausgangspunkt bei der Suche nach verallgemeinerten integrablen Modellen oder für störungstheoretische Methoden.

Frühe Arbeiten zu exakt lösbaren Modellen in der Physik stammen von Newton, Euler und Lagrange. Eine grosse Klasse integrabler Modelle wurde durch die Entdeckung der inversen Streumethode in den sechziger Jahren dieses Jahrhunderts zugänglich. Die folgende Aufzählung integrabler Systeme in den verschiedenen Bereichen der Physik ist bei weitem nicht vollständig und umfasst nur die bekanntesten bzw. wichtigsten Modelle.

In der klassischen Mechanik ist die einzige Paarwechselwirkung, für die sich das n-Teilchenproblem in 3 Raumdimensionen lösen lässt, durch das Potential des harmonischen Oszillators gegeben:

,.

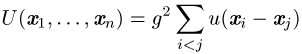Für eine beliebige Anzahl von Teilchen in einer Raumdimension sind die Bewegungsgleichungen zu folgenden Paarwechselwirkungspotentialen lösbar:

I) Calogero: ;

II) Sutherland:  bzw.;

III) , wobei  die Weierstrasssche -Funktion bezeichnet.

Integrable Verallgemeinerungen dieser Potentiale erhält man aus den Wurzelsystemen von Lie-Gruppen. Das Paarwechselwirkungspotential vom Typ II bleibt auch lösbar, wenn noch ein externes Exponentialpotential für jedes Teilchen addiert wird:.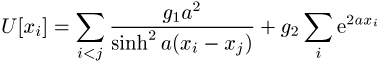

Schliesslich ist das allgemeine n-Teilchensystem noch für das Potential

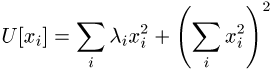
lösbar.

Weitere integrable Fälle der klassischen Mechanik sind:

1) ein Teilchen im beliebigen Zentralpotential, (Newton);

2) ein Teilchen in 3 Dimensionen im Zweizentren-Coulomb- bzw. Gravitationspotential,

 (Euler);

3) die freie Bewegung eines Punktes auf der Oberfläche eines 3-achsigen Ellipsoids (Jacobi) sowie d-dimensionale Verallgemeinerungen;

4) die Bewegung eines Massepunktes auf einer Kugel unter dem Einfluss einer linearen Kraft (Neumann);

5) die eindimensionale Bewegung von 3 Teilchen mit Paarwechselwirkung der Form

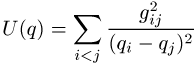 (Jacobi);

6) Spezialfälle für den 3-dimensionalen starren Körper mit festem Punkt (Kreisel) (Euler, Lagrange, Kowalewskaja) sowie d-dimensionale Verallgemeinerungen;

7) Spezialfälle für die Bewegung eines starren Körpers in einem idealen Fluid (Kirchhoff, Clebsch, Steklow).

Unter einem nichtlinearen Gitter versteht man nichtlineare Differenzengleichungen, wie sie für Teilchen auf einem Gitter mit Wechselwirkungen zwischen nächsten Nachbarn auftreten. Die bekanntesten integrablen Modelle für ein eindimensionales nichtlineares Gitter sind das Volterra-System mit den Bewegungsgleichungen

und das Toda-Gitter mit Hamiltonfunktion

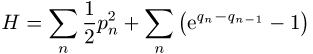
sowie diskrete Versionen des isotropen Heisenberg-Magneten sowie der nichtlinearen Schrödinger-Gleichung.

Zu den folgenden nichtlinearen eindimensionalen integrablen Feldgleichungen bzw. eindimensionalen Hamilton-Funktionalen sind Lax-Paare bekannt, und das Anfangswertproblem ist mit Hilfe der inversen Streumethode lösbar ():

die Korteweg-de-Vries-Gleichung (KdV)

,

die Sinus-Gordon-Gleichung

,

die Sinh-Gordon-Gleichung

,

die nichtlineare Schrödinger-Gleichung

,

der kontinuierliche Heisenberg-Magnet mit Hamilton-Funktion

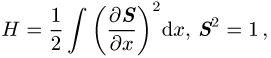
das Landau-Lifschitz-Modell für einen kontinuierlichen anisotropen Magneten

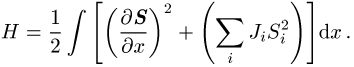
Zu den meisten dieser Gleichungen gibt es integrable Verallgemeinerungen, beispielsweise existieren zur KdV-Gleichung eine ganze Hierarchie von nichtlinearen Gleichungen mit Lax-Darstellungen sowie zweidimensionale Verallgemeinerungen (Kadomtsew-Petviashvili-Gleichung). Das Toda-Gitter oder die Sinus-Gordon-Theorie haben Verallgemeinerungen zu mehrkomponentigen Feldgleichungen, bei denen die Form der Potentiale wiederum mit den Wurzelsystemen von Lie-Gruppen zusammenhängen.

In der Quantenmechanik lässt sich die Schrödinger-Gleichung zu allen oben genannten n-Teilchenproblemen (I-III) der klassischen Mechanik, dem Toda-Gitter sowie deren Verallgemeinerungen, bei denen die inverse Streumethode anwendbar ist, lösen. Darüber hinaus sind die Vielteilchen-Schrödinger-Gleichungen für die Paarwechselwirkungspotentiale  und  lösbar. Das d-Potentialsystem ist äquivalent zur quantisierten nichtlinearen Schrödinger-Gleichung. Für ein einzelnes Teilchen in einem dreidimensionalen Zentralpotential lassen sich die Eigenwerte und Eigenfunktionen nur für den harmonischen Oszillator, das Coulomb-Potential, das Kastenpotential und das 1 / r⁴-Potential exakt angeben.

Die Eigenwerte und Eigenzustände für Drehimpuls-Zustände mit l = 0 bzw. für Teilchen in einer Dimension sind noch für eine Reihe von weiteren Potentialen bekannt, dazu zählen insbesondere (r = |x|)

1) die Eckart Potentiale:

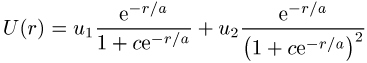
mit a ³ 0, c ³ -1. Bekannte Spezialfälle sind das Hulthén-Potential (u₂ = 0, c = -1) sowie das Hylleraas-Potential

.

2) .

Ein bekannter Spezialfall ist das Morse-Potential.

In der Quantenfeldtheorie lassen sich nur zu wenigen Theorien die Wightman-Funktionen angeben. Neben den freien Quantenfeldtheorien mit Lagrange-Dichten, in denen die Felder maximal quadratisch auftreten, handelt es sich dabei im allgemeinen um Theorien, in denen sich die Felder als einfache Funktionale freier Felder ausdrücken lassen, beispielsweise das masselose Thirring-Modell. Auch für eine grosse Klasse eindimensionaler konformer Feldtheorien kann man die Korrelationsfunktionen geschlossen angeben.

Mit Hilfe des Bethe-Ansatzes lassen sich die Eigenwerte und Eigenfunktionen der Hamilton-Operatoren unter anderem zur Sinus-Gordon-Gleichung, zur nichtlinearen Schrödinger-Gleichung, zum massiven Thirring-Modell, zum chiralen Gross-Neveu-Modell sowie zu verwandten Quantenfeldtheorien mit erweiterter innerer Symmetriegruppe berechnen.

In der statistischen Mechanik ist das zweidimensionale Ising-Modell (ohne äusseres Magnetfeld) das wohl bekannteste Beispiel eines integrablen Modells. Seine Lösung gelang Onsager 1944 durch Diagonalisierung der Transfermatrix. Mit Hilfe des Transfermatrix-Formalismus wurden auch das Sechs-Vertex-Modell (Lieb und Sutherland, 1967) und das Acht-Vertex-Modell (Baxter, 1971) sowie die dazu äquivalenten eindimensionalen Quantenspinketten des XXZ- und XYZ-Modells gelöst. Auch für diese Modelle gibt es eine grosse Anzahl integrabler Verallgemeinerungen mit internen Symmetrien. Für viele zweidimensionale statistische Modelle lassen sich am kritischen Punkt die Erwartungswerte mit Hilfe von Methoden aus der konformen Feldtheorie exakt bestimmen.

Literatur: L.D. Faddeev, L.A. Takhtajan, Hamiltonian Methods in the Theory of Solitons, Heidelberg 1987.
M.A. Olshanetsky und A.M. Perelomov, Classical integrable finite-dimensional Systems related to Lie algebras, Phys. Rep. 71 (1981).
M.A. Olshanetsky und A.M. Perelomov, Quantum integrable systems related to Lie algebras, Phys. Rep. 94 (1983).
R.J. Baxter, Exactly Solved Models in Statistical Mechanics, Academic Press 1982.