Techniklexikon

Kreisel

Symmetrischer Körper, der um eine Achse rotiert. Durch eine sog. kardanische Aufhängung wird er »kräftefrei«, er kann um zwei weitere Achsen »kippen«. In Rotation (meist hohe Drehzahlen) versetzt, behält die Drehachse ihre Lage im Raum bei. Der Einwirkung einer äußeren Kraft setzt der K. Widerstand entgegen, weicht aber senkrecht zu ihrer Angriffsrichtung aus. Diese Tatsache wird beim sog. Sensorkreisel genutzt, um Richtungen und Richtungsänderungen, z. B. eines Fahrzeugs, auf dem der K. montiert ist, zu messen und darzustellen (Kreiselkompaß). Mit sog. Arbeitskreiseln werden Plattformen im Raum stabilisiert, die in Flugzeugen und Raumfahrzeugen dann die Basis für Fluglageregelung und Navigation abgeben. Klassische Mechanik, im Sinne der Mechanik ein in einem Punkt, dem Rotationszentrum, festgehaltener, rotierender starrer Körper. Die Bewegungsgleichungen eines Kreisels unter dem Einfluss äusserer Kräfte sind die Eulerschen Gleichungen. Ohne äussere Kräfte (freier Kreisel) sind die Lösungen dieser Gleichungen bekannt. In diesem Fall sind die Energie E sowie der Drehimpuls L des Kreisels konstant. Die Richtung, die durch L bestimmt wird, heisst invariable Gerade. Bezeichnet man mit T den Trägheitstensor des Kreisels und mit W seine Winkelgeschwindigkeit, so gilt

sowie

Geometrisch besagt Gleichung (1), dass die Spitze von W auf der Oberfläche eines Ellipsoids, des Energieellipsoids, liegt. Gleichzeitig bewegt sich die Spitze von W wegen (2) in einer Ebene, die man invariable Ebene nennt und die einen konstanten Abstand zum Ursprung des Energieellipsoids hat. Sie steht senkrecht auf L und ist Tangentialebene des Energieellipsoids, d.h. die Spitze von W ist der Berührpunkt zwischen invariabler Ebene und Energieellipsoid. Man kann die Bewegung von W deshalb durch das Abrollen des Energieellipsoids auf der invariablen Ebene erhalten. Man nennt die Bahn, welche die Spitze von W auf der invariablen Ebene beschreibt, Herpholhodie oder Spurbahn, die entsprechende Bahn auf dem Energieellipsoid bezeichnet man als Polhodie oder Polbahn.

Für den sehr wichtigen Fall eines symmetrischen Kreisels, bei dem zwei der drei Hauptträgheitsmomente übereinstimmen, ist das Energieellipsoid rotationssymmetrisch. Beim Abrollen des Energieellipsoids auf der invariablen Ebene entstehen deshalb Kreise, d.h. W hat einen konstanten Betrag und beschreibt einen Kegel um L, der als Herpolhodiekegel oder Spurkegel bezeichnet wird. Die Bewegung der Symmetrieachse des Kreisels (Figurenachse) nennt man Nutation. W beschreibt einen Kegel um diese Symmetrieachse, der als Polhodiekegel oder Gangpolkegel bezeichnet wird. Die symmetrischen Kreisel lassen sich in zwei Typen unterteilen:

1) abgeplattet bezüglich der Figurenachse: das Trägheitsmoment bezüglich der Figurenachse ist grösser als die beiden anderen. In der Technik findet hauptsächlich dieser Kreiseltyp Verwendung.

2) verlängert bezüglich der Figurenachse: hier ist das Trägheitsmoment bezüglich der Figurenachse kleiner als die beiden anderen.

Beim unsymmetrischen Kreisel sind alle drei Hauptträgheitsmomente verschieden. In seinem körperfesten (also mit dem Kreisel mitrotierenden) Koordinatensystem bewegt sich die Spitze des Drehimpulsvektors auf einem Ellipsoid, dem sogenannten Drallellipsoid, und der Drehimpuls auf den Schnittlinien zwischen dieser Kugel und dem Drallellipsoid, wobei das Ende von L im gemeinsamen Ursprung von Kugel und Drallellipsoid festgehalten ist. Während Bewegungen um die Achse des grössten sowie kleinsten Hauptträgheitsmomentes stabil sind (freie Achsen), sind Drehungen um die Achse des mittleren Hauptträgheitsmomentes instabil.

Wirkt auf den Kreisel ein Drehmoment M ein, so versucht er, seine Achse so einzustellen, dass M und W in die gleiche Richtung zeigen. Dadurch führt der Drehimpuls bezüglich der Figurenachse L_F eine drehende Bewegung aus, die Präzession genannt wird. Ihr ist im allgemeinen noch eine Nutation der Figurenachse um L_F überlagert.

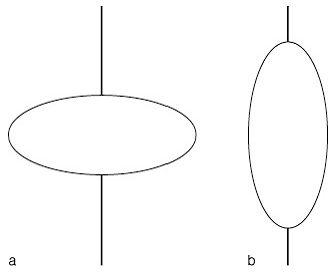
Kreisel: Beispiel für einen abgeplatteten (a) bzw. einen verlängerten symmetrischen Kreisel (b).