Techniklexikon

Arbeit

Bezeichnung für einen Begriff, der sich aus den Begriffen Kraft und Bahn (bzw. Weg) ableitet und in enger Beziehung zum Energiebegriff steht. Die SI-Einheit der Arbeit ist das Joule (J). (Energieeinheiten)

1) Mechanik: Wird ein Massenpunkt unter Aufwendung einer Kraft längs eines Weges verschoben, so wird hierbei Arbeit verrichtet. Die mathematische Definition der Arbeit ist , wobei F den Vektor der Kraft bezeichnet und dr das infinitesimale Element des Weges C, entlang dessen die Kraft wirkt. Man kann sagen, Arbeit sei das Wegintegral der Kraft. Arbeit wird im physikalischen Sinne nur von der Komponente der Kraft F verrichtet, die zum Wegelement dr parallel gerichtet ist. Aus dieser Definition folgt, dass eine Kraft, die einen Massepunkt nicht verschiebt (dr = 0), keine Arbeit leistet, und dass auch auf Wegen, die senkrecht zur Kraft verlaufen, keine Arbeit verrichtet wird.

Verläuft der Weg C im Spezialfall geradlinig und greift die Kraft stets im gleichen Winkel a an, dann wird aus dem Integral einfach das Skalarprodukt

W = F × Dr = FDrcos(a).

Das Vorzeichen der Arbeit ist so festgelegt, dass bei positivem W die Kraft selber Arbeit verrichtet, während bei negativem W gegen die Kraft Arbeit aufgewendet werden muss.

Der Zusammenhang zwischen Arbeit und Energie wird u.a. am Beipiel der Beschleunigungsarbeit deutlich. Wenn r(t) die Bahnkurve des Schwerpunktes eines Körpers der Masse m ist, so muss zur Beschleunigung des Körpers gemäss der dynamischen Grundgleichung die Kraft  aufgebracht werden, und für die Arbeit, die nötig ist, um den Körper von einer Geschwindigkeit ₁ auf eine Geschwindigkeit v₂ zu beschleunigen, ergibt sich

,

wobei E_kin,2 - E_kin,1 die Änderung der kinetischen Energie ist.

Die explizite Angabe des Weges ist im allgemeinen notwendig und kann nur dann fortgelassen werden, wenn die Arbeit in eindeutiger Weise nur vom Anfangs- und Endpunkt der Bewegung abhängt. Kraftfelder, für die dies gilt, werden als konservativ bezeichnet, und für sie lässt sich eine potentielle Energie  angeben. Die Arbeit für die Bewegung eines Massenpunktes von r₁ nach r₂ ist dann einfach die Potentialdifferenz zwischen diesen beiden Punken: , und längs eines beliebigen geschlossenen Weges verschwindet sie: .

Die an einem physikalischen System in einem konservativen Kraftfeld verrichtete Arbeit wird in dem System als potentielle Energie gespeichert und kann anschliessend als kinetische Energie wieder freigesetzt werden: So muss z.B. beim elastischen Dehnen einer Feder mit der Federkonstanten k um die Strecke x die der Bewegung entgegenwirkende Rückstellkraft kx überwunden werden. Dabei wird die Spannarbeit kx²/2 geleistet, die als potentielle Energie in der Feder gespeichert und beim Entspannen wieder zurückgewonnen wird.

Ein anderes Beipiel sind Bewegungen im Gravitationsfeld der Erde, bei dem es sich ebenfalls um ein konservatives Kraftfeld handelt. Wird ein Körper der Masse m in diesem Feld auf einem beliebigen Weg auf die Höhe h gehoben, so ist dazu die Hubarbeit W = F × h = mgh nötig. Diese Arbeit ist nicht verloren, der Körper hat vielmehr potentielle Energie E_pot gewonnen (man spricht auch von Lageenergie), die genau der Hubarbeit entspricht. Fällt der Körper zurück auf die Ausgangshöhe, so erreicht er dort die Geschwindigkeit  (Fallgesetze) und besitzt jetzt die kinetische Energie  (Reibung sei hier ausser acht gelassen).

Die für konservative Kraftfelder charakteristische Umwandlung von potentieller Energie in kinetische Energie und umgekehrt führt zum Energieerhaltungssatz der Mechanik. In realen Systemen spielen neben konservativen Kräften auch dissipative Kräfte (Reibung) und zeitabhängige Kräfte eine Rolle.

Für den Begriff der Arbeit ist die Zeit, während der die Arbeit verrichtet wird, unerheblich. Trotzdem kann es sinnvoll sein, die pro Zeiteinheit verrichtete Arbeit zu betrachten. Der Begriff, der dann ins Spiel kommt, ist die Leistung.

2) Elektrodynamik: Die Kraft auf eine Ladung in einem elektromagnetischen Feld berechnet sich zu . Das Magnetfeld B verrichtet keine Arbeit an der Ladung, da der entsprechende Kraftanteil stets senkrecht zur Bewegungsrichtung der Ladung steht. Da das elektrische Feld E konservativ ist, also gemäss  auf ein Potential f zurückgeführt werden kann, ergibt sich der allgemeine Ausdruck für die Arbeit der Bewegung einer Ladung im elektromagnetischen Feld als Produkt aus Ladung und Potentialdifferenz U:

Die elektrische Arbeit für den Fall stationärer Ströme folgt daraus zu , wobei  die elektrische Stromstärke und t die Dauer des Stromflusses ist. Allgemein ist die Arbeit eines beliebig zeitabhängigen elektrischen Stroms ; dies vereinfacht sich für harmonische Wechselspannungen  und  zu .

3) Thermodynamik: In der Thermodynamik wird der Kraftbegriff erweitert. Die verallgemeinerten Kräfte X_i werden analog zur Mechanik gemäss  definiert,

wobei die x_j äussere Parameter des Systems wie z.B. das Volumen, die Teilchenzahl des Systems oder ein äusseres Feld sind. Die bei einer infinitesimalen Änderung des Parameters x_i geleistete Arbeit ist dann , die Energieänderung dE beträgt entsprechend dem ersten Hauptsatz , in dem Q für die Wärme steht. Thermodynamisch kann die an einem System geleistete Arbeit also als Energieänderung durch Änderung der äusseren Parameter bei gleichzeitiger thermischer Isolierung, also bei konstantem Wärmeinhalt des Systems, definiert werden. Die Arbeit ist, gleich der Wärme eines Prozesses, im allgemeinen vom Weg des Prozesses im Raum der äusseren Parameter abhängig; sie stellt somit keine Zustandsfunktion dar, mit der man den Gleichgewichtszustand des Systems charakterisieren kann. Dementsprechend ist die Grösse , durch den Querstrich am Differentialsymbol gekennzeichnet, kein vollständiges Differential.

Der einfachste, zugleich auch der wichtigste Fall thermodynamischer Arbeit ist die Volumenänderungsarbeit, also die Arbeit, die bei einer Volumenänderung dx = dV gegen den Druck X = p verrichtet werden muss. Das thermodynamische System nimmt dabei bei quasistatischer Prozessführung die Arbeit  = pdV auf.

Ein anderes Beispiel für Arbeit im thermodynamischen Sinne ist diejenige, die ein elektrisches Feld bei der Polarisation eines Dielektrikums leistet. Sie hängt davon ab, welche Energieanteile man dem thermodynamischen System zurechnet. Es ergibt sich , wobei V das Volumen, E das elektrische Feld und D die dielektrische Verschiebung sind. In diesem Ausdruck ist sowohl der Energieanteil für die Polarisation des Mediums als auch derjenige für das elektrische Feld (im Vakuum) enthalten. Vernachlässigt man die Feldenergie, so ergibt sich wegen  die reine Polarisationsarbeit zu , wobei P für die Polarisation steht. Welcher Energieausdruck zu verwenden ist, hängt von der Fragestellung und der gegebenen experimentellen Situation ab.

Bei der Angabe der Arbeit, die ein Magnetfeld der Stärke H an einem magnetisierbaren Medium verrichten muss, um die Magnetisierung M aufzubauen, ist die Situation analog: Wird die Feldenergie mitberücksichtigt, so gilt . Bei Vernachlässigung der Feldenergie erhalten wir die reine Magnetisierungsarbeit zu , weil , wobei B die magnetische Induktion ist. Der Energieanteil des magnetischen Feldes spielt beim magnetokalorischen Effekt und der adiabatischen Entmagnetisierung eine entscheidende Rolle.

4) Quantenmechanik: Da der Arbeitsbegriff fest mit dem Kraftbegriff und mit dem Bahnbegriff verbunden ist, spielt er in der Quantenmechanik keine wesentliche Rolle, denn diese beiden Termini werden in der Quantenmechanik weitgehend aufgegeben. Man spricht lediglich z.B. etwas unpräzise von der Austrittsarbeit von Elektronen aus dem Atomverband.

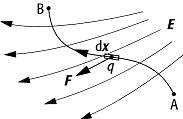
Arbeit 1: Zur Arbeit bei der Bewegung einer Ladung im elektrischen Feld.

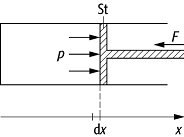
Arbeit 2: Zur Arbeit bei der Expansion eines Gases durch die Bewegung eines Kolbens.