Techniklexikon

Ising-Modell

Thermodynamik und statistische Physik, einfaches Gittermodell zur Beschreibung der magnetischen Eigenschaften eines Festkörpers. Den Punkten i eines d-dimensionalen Gitters wird als lokaler Freiheitsgrad eine Variable  zugeordnet, die manchmal auch als Spinvariable bezeichnet wird. Das Energiefunktional setzt sich zusammen aus Beiträgen direkt benachbarter Gitterpunkte ái,jñ sowie der Wechselwirkung der einzelnen magnetischen Momente mit einem äusseren Magnetfeld h:

.

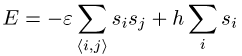Für e > 0 ist die parallele Ausrichtung der magnetischen Momente energetisch bevorzugt. Ist e < 0 so beschreibt das Modell einen Antiferromagneten (Antiferromagnetika), bei dem eine antiparallele Ausrichtung der Momente energetisch günstiger ist. Das Modell gibt die allgemeine Phasenstruktur eines Ferromagneten recht gut wieder, insbesondere besitzt es für h = 0 in mehr als zwei Dimensionen einen Phasenübergang zweiter Ordnung von einer ungeordneten Hochtemperaturphase zu einer geordneten (magnetisierten) Tieftemperaturphase.

Andere Anwendungen des Ising-Modells ergeben sich durch Uminterpretation der beiden Spin-Freiheitsgrade s. So beschreibt das Ising-Modell beispielsweise auch zweikomponentige Legierungen. s = +1 bezeichnet Komponente A, s = -1 Komponente B einer AB-Legierung. h übernimmt die Bedeutung eines chemischen Potentials. Die geordnete Phase entspricht einer Agglutination beider Komponenten, die ungeordnete Phase einem gegenseitigen Durchdringen. Ein weiters Beispiel ist das des Gittergases. Der Zustand s = +1 kennzeichnet einen besetzten Gitterplatz, s = -1 einen unbesetzten Gitterplatz. Wiederum kann h mit dem chemischen Potential in Beziehung gebracht werden. Die geordnete Phase entspricht hier einer kondensierten Phase, die ungeordnete Phase einem Gas.

Das Ising-Modell ist der Prototyp eines Gittermodells. Es wird 1920 zum ersten Mal in einer Arbeit von Lenz erwähnt, im Anschluss daran von seinem späteren Mitarbeiter E. Ising und 1925 in dessen Doktorarbeit näher untersucht. 1936 bewies Peierls die Existenz zweier Phasen in mehr als zwei Dimensionen. Die kritische Temperatur des zweidimensionalen Modells wurde 1941 von Kramers und Wannier exakt zu

berechnet. 1944 gelang Onsager die Berechnung der Zustandssumme für das zweidimensionale Ising-Modell ohne äusseres Magnetfeld durch Diagonalisierung der Transfermatrix. Seither wurden viele Verfahren gefunden, die freie Energie dieses Modells exakt zu berechnen. Bekannt ist unter anderem die Methode von Feynman, bei der die Zustandssumme aus ihrer Darstellung als Summation über geschlossene Wege bestimmt wird.

Die spezifische Wärme besitzt am kritischen Punkt eine logarithmische Singularität. Am kritischen Punkt verhalten sich die Korrelationsfunktionen des zweidimensionalen Ising-Modells wie die eines eindimensionalen Gases freier Fermionen.

Für mehr als zwei Dimensionen sind bis heute keine exakten Lösungen bekannt, allerdings existieren sehr gute Hoch- bzw. Tieftemperaturentwicklungen, aus denen sich die kritischen Exponenten beispielsweise mit Hilfe von Padé-Approximationen bestimmen lassen. In mehr als vier Dimensionen stimmen die kritischen Exponenten mit den Vorhersagen einer Molekularfeldnäherung überein.

Ising-Modell 1: Spinkonfiguration in einem 2-dimensionalen Ising-Modell: a) Ungeordnete Konfiguration bei Temperaturen T > T_c; b) bei T = T_c existieren bereits korrelierte Bereiche mit endlicher Grösse.

Ising-Modell 2: Schematische Darstellung: a) Ungeordnete Konfiguration bei hohen Temperaturen; b) Langreichweitige Korrelationen bei tiefen Temperaturen.