Techniklexikon

Transfermatrix

Thermodynamik und statistische Physik, Matrix, die sich zu vielen Gittermodellen in der statistischen Mechanik so konstruieren lässt, dass die freie Energie des Systems durch den höchsten Eigenwert dieser Matrix gegeben ist. Allgemeiner lässt sich die Zustandssumme des Modells auf einem endlichen Gitter (Länge L) mit periodischen Randbedingungen als Spur der L-ten Potenz dieser Transfermatrix schreiben. Über die Transfermatrix sind auch d-dimensionale klassische Gittermodelle mit (d - 1)-dimensionalen Quantenmodellen (Quantenspinketten) verknüpft. Viele statistische Modelle, darunter das Ising-Modell, das Sechs-Vertex-Modell und das Acht-Vertex-Modell, wurden ursprünglich mit Hilfe der Transfermatrix gelöst. Die Beziehung zwischen der Transfermatrix eines Gittermodells und seiner Zustandssumme ist vergleichbar mit der Beziehung zwischen dem Hamilton-Formalismus einer Quantentheorie und dem Funktionalintegral zu dieser Theorie.

Anhand eines einfachen Spin-Modells mit der Energie  sei die Idee des Transfermatrixformalismus erläutert. Das d-dimensionale Gitter  wird zunächst in »Schichten« von (d - 1)-dimensionalen Untergittern  zerlegt, so dass . Sei H der Vektorraum der komplexwertigen Funktionen von den Spinkonfigurationen auf dem Gitter . (H entspricht dem Hilbert-Raum der Quantenmechanik, d.h. dem Raum der komplexwertigen Funktionen über den Konfigurationen von Teilchen. Auf die Definition des Skalarprodukts und die Einschränkung auf normierbare Funktionen soll hier nicht eingegangen werden.) Eine Basis dieses Vektorraums ist durch  gegeben, wobei  die Gitterpunkte von  durchnumeriert und {s_n} alle möglichen Konfiguration der Spins auf diesem Untergitter durchläuft. Die Transfermatrix ist eine lineare Abbildung auf H und wird zwei benachbarten Schichten mit Konfigurationen {s_n} und  zugeordnet. Sie ist definiert durch ihre Matrixelemente in der oben angegebenen Basis von H und entspricht im wesentlichen dem Beitrag dieser beiden Schichten zum Boltzmann-Faktor:

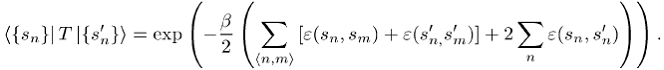
Für die Zustandssumme lässt sich dann leicht zeigen

und im thermodynamischen Grenzfall

 folgt für die freie Energiedichte

wobei l_max der maximale Eigenwert der Transfermatrix ist. Über  (mit einer geeignet zu wählenden Gitterkonstanten a) lässt sich eine Matrix H definieren, die als Hamilton-Operator des zugehörigen (d - 1)-dimensionalen Quantensystems aufgefasst werden kann.

Der Transfermatrixformalismus ersetzt somit ein kombinatorisches Problem – die Berechnung einer Zustandssumme – durch ein algebraisches Problem – die Berechnung eines Eigenwerts. Auch wenn für zwei- und mehrdimensionale Gittermodelle die Grösse der Transfermatrix exponentiell mit der Anzahl der Gitterpunkte des (d - 1)-dimensionalen Untergitters anwächst, helfen oftmals Symmetrien des Systems bei der Diagonalisierung der Matrix.