Techniklexikon

Morse-Potential

Chemie, Physikalische Chemie, Morse-Funktion, empirisch von P.M. Morse gefundene Potentialfunktion, die die tatsächliche Abhängigkeit der potentiellen Energie E_p zweier Atome von ihrem Abstand r recht gut wiedergibt. Nach Morse können asymmetrische Energiekurven von Molekülen oft durch folgende Funktion angenähert werden:  (D ist die Dissoziationsenergie der Bindung zwischen beiden Atomen oder Tiefe des Potentialminimums, r ist der Molekülabstand, r₀ der Gleichgewichtsabstand der Atome, a ist eine für die Krümmung der Energiekurve massgebende Konstante mit dem Wert a = (m / 2D)^{1 / 2}n₀; m ist die reduzierte Masse des Systems, n₀ die Grundfrequenz des Moleküls). Wenn man die Morse-Funktion als potentielle Energie in der Schrödinger-Gleichung verwendet, dann entsprechen die für den Oszillator erhaltenen Energieniveaus jenen des anharmonischen Oszillators (Anharmonizität). Der Abstand dieser Energieniveaus ist nicht äquidistant, sondern wird mit zunehmender Quantenzahl v kleiner. Die Abnahme des Abstandes zwischen aufeinanderfolgenden Niveaus ist dabei konstant. Die Anzahl der Niveaus bis zur Dissoziationsgrenze ist endlich. In der Abbildung ist die Morse-Funktion graphisch aufgetragen. Man erkennt, dass sich die beiden Atome selbst bei grosser Schwingungsenergie und damit sehr grosser Schwingungsamplitude nicht beliebig weit nähern können. Die Coulomb-Abstossung zwischen den beiden Atomkernen verhindert dies. Weil der rechte Ast der Potentialkurve in eine Horizontale übergeht, kann es bei hoher Schwingungsanregung zu einer Dissoziation des zweiatomigen Moleküls kommen. Die Energiedifferenz zwischen dem Minimum der Kurve und dem horizontalen Ast ist gleich der Dissoziationsenergie. Oberhalb der Dissoziationsenergie ist die Energie nicht mehr gequantelt. Dort liegt ein Energiekontinuum vor.

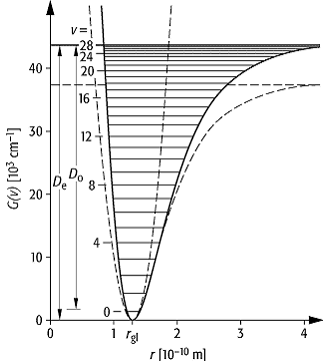
Morse-Potential: Aufgetragen ist die Morse-Funktion mit v Energieniveaus in Abhängigkeit vom Kernabstand r. D₀ ist die Dissoziationsenergie zum Kernabstand des Maximums der Eigenfunktion für den Schwingungszustand v = 0, r_gl ist der Gleichgewichtsabstand und entspricht dem Minimum der Potentialkurve. Die zugehörige Dissoziationsenergie ist D_e.