Techniklexikon

Drehimpuls

Klassische MechanikQuantenmechanik 1) Mechanik: (veraltet: Drall, Impulsmoment), grundlegender Begriff der Mechanik des Massepunktes und des starren Körpers. Der Drehimpuls ist definiert als das Vektorprodukt  des Ortsvektors r bezüglich eines beliebigen Bezugsspunktes und des Impulses p. Er kann in der SI-Einheit N × m × s angegeben werden. Der Drehimpuls gehört zu den Bewegungsintegralen der Mechanik; für abgeschlossene, allgemein für beliebige rotationsinvariante Systeme ist er eine Erhaltungsgrösse (Drehimpulserhaltungssatz).

Der Drehimpuls eines Systems von Massenpunkten ergibt sich als lineare Summe der Einzeldrehimpulse: . Für eine kontinuierliche Massenverteilung mit der Dichte r, z.B. für einen starren Körper, wird dies zu , wobei  das aus dem Volumenelement dV und der Dichte r zusammengesetzte Massenelement ist. Im Schwerpunktsystem des Körpers kann man den Drehimpuls als  schreiben; V steht hier für den Trägheitstensor, w für den Vektor der Winkelgeschwindigkeit.

Im allgemeinen hängt der Drehimpuls vom Bezugssystem ab. Sind K und K ¢ zwei Bezugssysteme, deren Ursprünge um die Strecke a voneinander entfernt sind, so besteht zwischen den Ortsvektoren r und r ¢ ein und desselben Punktes die Beziehung r = r ¢ + a, und für den Drehimpuls ergibt sich . Dabei ist  der Gesamtimpuls des Systems (Impuls). Der Drehimpuls ist somit nur dann unabhängig vom Bezugssystem, wenn der Gesamtimpuls P verschwindet, das System als Ganzes also ruht. Handelt es sich bei K und K ¢ um zwei Inertialsysteme, wobei K ¢ das Schwerpunktsystem sei, und bewegt sich das eine mit einer Geschwindigkeit  v  relativ zum anderen, so erhält man für den Gesamtdrehimpuls des Systems  (mit dem Ortsvektor R des Schwerpunktes). Der Gesamtdrehimpuls des Körpers in einem beliebigen Bezugssystem setzt sich also aus dem Eigendrehimpuls L ¢  (im Schwerpunktsystem) und dem von der Schwerpunktsbewegung als Ganzes herrührenden Bahndrehimpuls  zusammen.

In einer mehr mathematischen Betrachtungsweise kann der Drehimpuls als die infinitesimale Erzeugende der räumlichen Drehungen betrachtet werden, die die Lie-Gruppe SO(3) bilden; der Zusammenhang zwischen dieser Sichtweise und der obigen physikalischen Definition wird im Rahmen des Konzepts der kanonischen Transformationen (analytische Mechanik) offensichtlich.

2) Quantenmechanik: Durch Quantisierung, das heisst durch Ersetzen der Orts- und Impulskomponenten x_i und p_j durch hermitesche lineare Operatoren , die den Vertauschungsrelationen  und  genügen, entstehen dadurch für die Komponenten  des Operators , in der Quantenmechanik auch als Bahndrehimpulsoperator bezeichnet, die Vertauschungsrelationen  (e_ijk: Levi-Civita-Symbol). Die einzelnen Drehimpulskomponenten vertauschen also nicht miteinander; dies bedeutet, dass nicht alle drei Komponenten simultan gemessen werden können (siehe unten). Da in der Quantenmechanik auch andere Drehimpulsoperatoren, wie zum Beispiel der Spin, auftreten, muss der Begriff des Drehimpulses in der Quantenmechanik verallgemeinert werden. Man bezeichnet hier einen Operator , dessen Komponenten  den Kommutationsrelationen  gehorchen, als Drehimpulsoperator. Die Operatoren  spannen eine Lie-Algebra, die sog. Drehimpulsalgebra, auf. Anhand der Kommutationsrelationen erkennt man, dass die Drehimpulsalgebra isomorph zu den Lie-Algebren  ist. Der einzige Casimir-Operator der Drehimpulsalgebra ist der Beltrami-Operator .

In der Quantenmechanik werden häufig Systeme betrachtet, die eine Rotationssymmetrie besitzen; dann gilt ; D ist dabei eine Darstellung der Drehgruppe auf dem quantenmechanischen Hilbert-Raum H, R eine beliebige Drehung, also ein Element der zugrunde liegenden Drehgruppe (Darstellung einer Gruppe). Betrachtet man die stationäre Schrödinger-Gleichung , wobei die  Eigenvektoren zum Energie-Eigenwert E_n sind, die durch i entartet sein können, so folgt aus der Invarianz des Systems unter Drehungen, dass die D(R)y_n,i für eine beliebige Drehung R wieder Eigenvektoren zum Energie-Eigenwert E_n sind. Der durch Anwendung aller Drehungen D(R) auf y_n,i erzeugte Raum besitzt eine irreduzible Darstellung der Drehgruppe, da er aufgrund seiner Konstruktion keine invarianten Unterräume bezüglich der Drehungen besitzt (Darstellung einer Gruppe). Aus diesem Grund interessiert sich die Physik für die irreduziblen Darstellungen der Drehgruppe und somit für die irreduziblen Darstellungen der zugehörigen Drehimpulsalgebra.

Die irreduziblen Darstellungen der Drehimpulsalgebra werden nach Eigenwerten des Casimir-Operators  und der Cartan-Unteralgebra, die o.B.d.A. durch  aufgespannt wird, definiert. Physikalisch entspricht dies der Tatsache, dass aufgrund der Kommutationsrelationen die einzelnen Komponenten des Drehimpulsoperators nicht simultan messbar sind. Dagegen sind der Beltrami-Operator  und eine Komponente des Drehimpulsoperators  simultan messbar. Man wählt deshalb eine beliebige Drehimpulskomponente, üblicherweise , aus und betrachtet eine Basis des Darstellungsraumes, die aus Eigenvektoren der Operatoren  und  bestehen. Die Eigenvektoren werden mit  bezeichnet, die den Eigenwertgleichungen  und  genügen, wobei man j als Drehimpulsquantenzahl und m als magnetische Quantenzahl bezeichnet; letztere Benennung stammt aus der Atomphysik. Man definiert die Leiteroperatoren  und  mit den Kommutationsrelationen  . Aus den Kommutationsrelationen folgt, dass  und . Dabei gilt für die Quantenzahlen, dass  und m =  - j, - j + 1,...,j - 1, j. Somit ist jeder irreduzible Darstellungsraum, der durch eine Drehimpulsquantenzahl j beschrieben wird, (2j + 1)-fach entartet. Man bezeichnet diese Eigenschaft als Richtungsentartung.

Wird jedoch die Rotationssymmetrie des physikalischen Systems beispielsweise durch ein äusseres Magnetfeld gebrochen, so kann der quantenmechanische Drehimpuls keine beliebigen Werte annehmen, sondern sich zu jeder Drehimpulsquantenzahl j nur in 2j + 1 verschiedene Richtungen einstellen (Richtungsquantisierung, Richtungsquantelung, räumliche Quantelung).

In der Ortsdarstellung hat der Bahndrehimpulsoperator die Form , woraus sich in Kugelkoordinaten

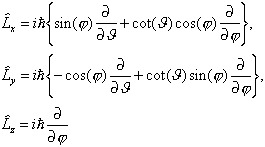
und für den Beltrami-Operator

ergibt. Die zugehörigen Eigenvektoren  sind die Kugelflächenfunktionen Y_lm(J,f), wobei nur ganzzahlige Drehimpulsquantenzahlen l, also  auftreten. Die halbzahligen Drehimpulsquantenzahlen werden in der Quantenmechanik durch den Spin beschrieben. Die Komponenten des Spinoperators  erfüllen ebenfalls die Kommutationsrelationen der Drehimpulsalgebra, haben jedoch die Eigenvektoren  mit halbzahligen Eigenwerten . [MM1]