Techniklexikon

Lie-Gruppe

in der Physik wichtige mathematische Gruppe, deren Elemente differenziebare Funktionen der Parameter sind und sich durch die Exponential-Funktion

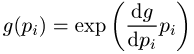
erzeugen lassen, d.h. jedes Gruppenelement ergibt sich aus der gewichteten Summe einer endlichen Anzahl von Erzeugenden (Generatoren), wobei diese Anzahl der Ordnung der entsprechenden Lie-Gruppe entspricht. Von besonderem physikalischen Interesse sind folgende Lie-Gruppen:

a) : komplexe allgemeine lineare Gruppe aller invertierbaren komplexen -Matrizen, .

b) : allgemeine lineare Gruppe aller invertierbaren reellen -Matrizen, .

c) : Gruppe der komplexen -Matrizen  mit , .

d) : Gruppe der unitären -Matrizen ; .

e) : Gruppe der unitären -Matrizen  mit ; .

f) : Gruppe der Drehungen des euklidischen , das ist die Gruppe aller reellen -Matrizen , so dass  und ; .  ist die universelle Überlagerungsgruppe der Drehgruppe  (Spinor);

g) Lorentzgruppe, d.h. die Gruppe aller reellen -Matrizen, die die Minkowski-Metrik invariant lassen; ; ihre universelle Überlagerungsgruppe ist  (Spinor).(Lie-Algebra, Darstellung einer Gruppe, Symmetrien)