Techniklexikon

Quantengravitation

Relativitätstheorie und Gravitation

bottom:.0001pt\'>Quantengravitation bezeichnet allgemein die Beschreibung der gravitativen Wechselwirkung im Rahmen einer Quantentheorie. Im besonderen versteht man darunter eine Theorie, welche Allgemeine Relativitätstheorie und Quantentheorie konsistent zusammenführt. Eine solche Theorie liegt noch nicht in einer vollendeten Form vor, doch gibt es vielversprechende Ansätze, welche wichtige Aspekte erkennen lassen. Insbesondere werden Aussagen über die Quanteneigenschaften von Raum und Zeit getroffen. Obwohl bisher weit von einer direkten experimentellen Überprüfung entfernt, ist eine Theorie der Quantengravitation unverzichtbar für ein grundlegendes Verständnis der Natur. Es gibt Spekulationen, wonach eine Quantengravitation notwendigerweise eine Vereinheitlichung aller Wechselwirkungen nach sich zieht.

bottom:.0001pt\'> 

bottom:.0001pt\'>Einleitung

bottom:.0001pt\'>Nach gegenwärtigen Erkenntnissen gehorcht die gesamte Physik der Quantentheorie. Starke und elektroschwache Wechselwirkung werden erfolgreich durch Quantenfeldtheorien beschrieben. Abseits steht bisher nur die gravitative Wechselwirkung, deren theoretischer Rahmen die Allgemeine Relativitätstheorie ist, eine sowohl begrifflich klare als auch experimentell äusserst erfolgreiche Theorie. Im folgenden soll begründet werden, warum dieser heterogene begriffliche Zustand der Physik nicht fundamental richtig sein kann. Zunächst werden die Gründe diskutiert, die für die Quantennatur des Gravitationsfeldes sprechen. Dann wird eine kurze Übersicht über die Schwierigkeiten gegeben, welche bei der Konstruktion einer Theorie der Quantengravitation auftreten. Das betrifft sowohl Probleme begrifflicher Art wie das Zeitproblem als auch Probleme mathematischer Art, etwa das Problem der Regularisierung. Danach wird ein Zugang, die kanonische Quantisierung der Allgemeinen Relativitätstheorie, kurz vorgestellt. Einem anderen Zugang, der String-Theorie, ist ein eigener Essay gewidmet. Schliesslich sollen der Anwendungsbereich einer Theorie der Quantengravitation und die Möglichkeit ihrer experimentellen Überprüfbarkeit diskutiert werden.

bottom:.0001pt\'> 

bottom:.0001pt\'>Warum Quantengravitation?

bottom:.0001pt\'>Welche Gründe sprechen für eine Quantisierung der Gravitation? Im Gegensatz zur Newtonschen Gravitationstheorie benennt die Allgemeine Relativitätstheorie ihre eigenen Grenzen: Unter allgemeinen Voraussetzungen lassen sich Singularitätentheoreme beweisen, die besagen, dass bestimmte Geodätische nicht über einen gewissen Punkt der Raumzeit hinweg fortgesetzt werden können, die Raumzeit dort gewissermassen »endet«. Es muss sich dabei nicht um eine Singularität in der Krümmung handeln, obwohl eine solche in interessanten Fällen vorliegt - im Inneren Schwarzer Löcher und am Urknall. Eine umfassendere Theorie ist also vonnöten, um diese Bereiche konsistent beschreiben zu können; obwohl logisch nicht zwingend, so ist es doch naheliegend, hierfür eine Quantengravitation anzunehmen - so hat auch schon die gewöhnliche Quantenmechanik die klassische Instabilität des Atoms beseitigt.

bottom:.0001pt\'>Mit der Urknallsingularität hängt das Problem der Anfangsbedingungen in der Kosmologie zusammen - die Entwicklung des Universums kann nur dann völlig verstanden werden, wenn die Singularität am Urknall vermieden wird. Eine Theorie der Quantenkosmologie erhebt den Anspruch, dies zu leisten.

bottom:.0001pt\'>Während diese Argumente eher von der gravitativen Seite herrühren, gibt es auch eine Reihe von Argumenten, die von der Quantentheorie ausgehen. Da ist zunächst einmal die Tatsache, dass alle bekannten nichtgravitativen Wechselwirkungen erfolgreich durch Quantentheorien beschrieben werden. Im Lichte der Vereinheitlichungsbestrebungen der modernen Physik sollte dies auch auf die Gravitation zutreffen, da sie an alle anderen Felder gekoppelt ist. In der Tat ist die String-Theorie eine Theorie, die den Anspruch erhebt, eine vereinheitlichte Quantentheorie aller Wechselwirkungen (notwendig auch der Gravitation) zu sein. Ansätzen, welche versucht haben, ein klassisches Gravitationsfeld konsistent an Quantenfelder zu koppeln, war bisher kein Erfolg beschieden.

bottom:.0001pt\'>Ein weiteres Argument geht auf Wolfgang Pauli zurück: Die Einbeziehung der Gravitation könnte erreichen, dass die in der Quantenfeldtheorie vorhandenen Divergenzen automatisch beseitigt werden. Das liegt daran, dass diese Unendlichkeiten von der Struktur der Raumzeit auf kleinsten Skalen herrühren und eine Quantengravitation gerade zu diesem Bereich Aussagen treffen soll. In der Tat scheinen dies einige der bisherigen Versuche (String-Theorie, kanonische Quantengravitation) bewerkstelligen zu können.

bottom:.0001pt\'>Eine Theorie der Quantengravitation ist von unmittelbarer Bedeutung für die Kosmologie. Wegen der quantenmechanischen Nichtseparabilität ist es im allgemeinen unmöglich, einem Subsystem einen eigenen (reinen) Quantenzustand zuzuordnen, da es mit Freiheitsgraden seiner Umgebung korreliert ist (Dekohärenz (Kohärenz), Messprozesse in der Quantenmechanik). Diese Freiheitsgrade sind wiederum an ihre Umgebung gekoppelt, so dass in letzter Konsequenz nur das Universum als Ganzes abgeschlossen ist und einen eigenen reinen Quantenzustand besitzt, die »Wellenfunktion des Universums«. Das Universum muss somit im Rahmen einer Quantenkosmologie beschrieben werden.

bottom:.0001pt\'>Auf welcher Skala wären direkte Effekte der Quantengravitation zu erwarten? Das sollte ganz sicher dann der Fall sein, wenn die von einem quantenmechanischen Objekt (»Elementarteilchen«) hervorgerufene Raumzeitkrümmung nicht mehr vernachlässigbar klein ist. Hat das Teilchen die Masse m, so ist die typische quantenmechanische Skala die Compton-Wellenlänge  (Compton-Effekt). Setzt man diese gleich dem aus der Allgemeinen Relativitätstheorie bekannten Schwarzschild-Radius , so erhält man (ein Faktor 2 sei vernachlässigt) die sogenannte Planck-Masse  In den Einheiten der Elementarteilchenphysik entspricht das der enormen Masse von etwa 10¹⁹ GeV. Die zugehörigen Längen- und Zeitskalen sind die Planck-Länge  bzw. die Planck-Zeit . M. Planck stellte diese Einheiten 1899 auf (siehe [20]Abb. 1). Er konnte das vor der Einführung des Wirkungsquantums tun, da  in das aus der Erfahrung bekannte Wiensche Gesetz eingeht. (Vor ihm hatte bereits Johnstone Stoney ähnliche Einheiten betrachtet.)

bottom:.0001pt\'>Welche Schwierigkeiten stehen der Konstruktion einer Quantengravitation entgegen? Das vielleicht grösste Problem besteht darin, dass derzeit noch keine Experimente zur Verfügung stehen, für die eine solche Theorie relevant wäre. Ein Beschleuniger, der Strukturen auf der Skala der Planck-Länge enthüllen sollte, müsste galaktische Dimensionen aufweisen. Allerdings entscheidet die Theorie darüber, was beobachtbar ist, weshalb mögliche Tests von ganz anderer Natur sein können (siehe unten).

bottom:.0001pt\'>Eine grosse theoretische Herausforderung besteht natürlich darin, die richtige Methode anzuwenden. Es hat sich in anderen Fällen bewährt, eine Quantentheorie durch Anwendung heuristischer »Quantisierungsregeln« auf eine vorgegebene klassische Theorie zu erraten, z.B. bei der Quantenelektrodynamik. Ein ganz anderes (spekulatives) Programm versucht, direkt eine fundamentale Quantentheorie aller Wechselwirkungen zu konstruieren und hieraus die gravitative Wechselwirkung in einem geeigneten Grenzfall abzuleiten. Diesen Anspruch hat etwa die String-Theorie. Die Schwierigkeit besteht dabei freilich darin, dass die Eindeutigkeit des Ausgangspunktes (die vorgegebene klassische Theorie) verlorengeht. Auch bei Beschränkung auf die erste Methode ist a priori nicht klar, welche der klassischen Strukturen »quantisiert« werden sollen und welche als nichtdynamische Hintergrundstrukturen in der Quantentheorie überleben. Chris Isham hat die folgende Hierarchie von Strukturen einer Raumzeit erstellt, bei der diese Frage auf jeder Ebene gestellt werden kann:

bottom:.0001pt\'>Lorentzsche Mannigfaltigkeit  Kausale Mannigfaltigkeit (»Lichtkegel«)  Differenzierbare Mannigfaltigkeit  Topologischer Raum  Ereignismenge.

bottom:.0001pt\'>Die meisten Zugänge »quantisieren« nur die beiden ersten Strukturen (d.h. wenden nur hierauf das Superpositionsprinzip an), tasten also die klassische Struktur einer differenzierbaren Mannigfaltigkeit nicht an. Das bedeutet freilich nicht, dass die fertige Theorie der Auflösung beliebig kleiner raumzeitlicher Distanzen operationelle Bedeutung beimisst (siehe unten). Auf jeden Fall zeigt sich bei diesen Betrachtungen das Hauptproblem jedes Zuganges: Die Raumzeit ist keine feste Hintergrundstruktur wie bei nichtgravitativen Theorien, sondern spielt eine dynamische Rolle. Schon Pauli hat behauptet: »Es scheint mir..., dass nicht so sehr die Linearität oder Nichtlinearität Kern der Sache ist, sondern eben der Umstand, dass hier eine allgemeinere Gruppe als die Lorentz-Gruppe vorhanden ist...«

bottom:.0001pt\'>Als Hauptzugänge zur Quantengravitation gelten insbesondere String-Theorie (»M-Theorie«) und quantisierte Allgemeine Relativitätstheorie. Selbst wenn die String-Theorie die fundamental korrekte Theorie darstellt, so kommt doch der quantisierten Allgemeinen Relativitätstheorie grosse Bedeutung zu: Sie sollte nämlich als effektive Theorie auf Längenskalen grösser als die Planck-Länge richtig sein, wie auch etwa das Standardmodell der Teilchenphysik als effektive Theorie für kleine Energien gültig ist. Ihr Konzept und ihre Probleme seien im folgenden kurz skizziert.

bottom:.0001pt\'> 

bottom:.0001pt\'>Quantisierung der Allgemeinen Relativitätstheorie

bottom:.0001pt\'>Bei diesem Zugang werden bewährte »Quantisierungsregeln« auf die Allgemeine Relativitätstheorie angewandt, wobei zwischen kovarianten und kanonischen Zugängen zu unterscheiden ist.

bottom:.0001pt\'>In kovarianten Zugängen spielt die vierdimensionale Mannigfaltigkeit der Raumzeit eine fundamentale Rolle. Üblicherweise versucht man - in Anlehnung an andere Quantenfeldtheorien -, einen störungstheoretischen Aufbau der Theorie, wobei die vierdimensionale Metrik  um eine feste Hintergrundmetrik  entwickelt und die Abweichung durch die Gravitationskonstante G parametrisiert wird:

bottom:.0001pt\'>

bottom:.0001pt\'>Es werden dann für  Feynman-Regeln abgeleitet. In manchen Hintergrundraumzeiten (z.B. Minkowski-Raum oder De-Sitter-Raum) werden durch  Spin 2-Teilchen (»Gravitonen«) beschrieben, die vor dem durch  gegebenen festen Hintergrund propagieren. Mit dem kovarianten Zugang sind vor allem zwei Probleme verbunden: Zum einen ist die Störungstheorie nichtrenormierbar, d.h. in jeder Ordnung erscheinen neuartige Divergenzen, welche insgesamt die Einführung von unendlich vielen Parametern verlangen, welche dem Experiment entnommen werden müssen. Formal liegt das daran, dass  dimensionslos ist ( bezeichnet den einer Feynman-Linie zugeordneten Cutoff-Impuls) und deshalb in beliebig hohen Potenzen erscheinen kann. Zum anderen wird der Begriff der kausalen Abhängigkeit raumzeitlicher Ereignisse problematisch, da man zeigen kann, dass es für je zwei Punkte mindestens eine Metrik gibt, bezüglich der diese Punkte nicht raumartig sind: Da in der Quantengravitation alle Metriken beitragen, wird der für die normale Quantenfeldtheorie relevante Begriff der Mikrokausalität (Lokalität) fragwürdig. Aus diesen Gründen erfreut sich der kovariante Zugang nicht mehr allzu grosser Beliebtheit, auch wenn er als effektive Theorie von Nutzen ist. Das gilt ebenfalls für eine Spielart des kovarianten Zuganges, die mit dem Begriff des Pfadintegrales arbeitet, obwohl Pfadintegrale gelegentlich dazu herangezogen werden, Randbedingungen für die kanonische Theorie (no boundary-Vorschlag von Hartle und Hawking) zu liefern.

bottom:.0001pt\'>Bei kanonischen Zugängen zur Quantengravitation kommt nur dem dreidimensionalen Raum eine fundamentale Rolle zu. Die einzelnen Versionen unterscheiden sich darin, welche kanonisch-konjugierten Variablen (verallgemeinerte Orte und Impulse) auf dem Raum gewählt werden. In der traditionellen Formulierung der Geometrodynamik handelt es sich um die dreidimensionale Metrik  und den konjugierten Impuls , welcher eine lineare Funktion der äusseren Krümmung ist. Letztere gibt in der klassischen Theorie an, wie der dreidimensionale Raum in die vierdimensionale Raumzeit eingebettet ist. Eine neuere Formulierung, welche auf Abhay Ashtekar zurückgeht, benutzt als kanonische Variablen einen SU(2)-Zusammenhang  und als zugehörigen Impuls das (in eine räumliche Dichte verwandelte) Dreibein . Aus dieser Zusammenhangsdynamik erhält man die Schleifendynamik, wenn man statt  dessen Holonomien (»Wilson-Schleifen«) wählt, bei welcher der Zusammenhang über alle Schleifen integriert wird.

bottom:.0001pt\'>Wendet man den kanonischen Formalismus auf die Allgemeine Relativitätstheorie an, so ergeben sich Zwangsbedingungen, welche die kanonischen Variablen miteinander in Beziehung setzen, ohne dass zweite zeitliche Ableitungen vorkommen. Das Auftreten solcher Zwangsbedingungen ist eng mit den Invarianzeigenschaften einer Theorie verknüpft. In der Allgemeinen Relativitätstheorie gibt es die vierparametrige Gruppe der Koordinatentransformationen (bzw. aktiv aufgefasst der Diffeomorphismen), weshalb man (pro Raumpunkt) vier Zwangsbedingungen findet: Die mit der Invarianz unter Reparametrisierungen der Zeitkoordinate verknüpfte Hamiltonsche Zwangsbedingung

bottom:.0001pt\'>

bottom:.0001pt\'>sowie die drei mit der Invarianz unter Reparametrisierungen der räumlichen Koordinaten verknüpften  Impuls-Zwangsbedingungen

bottom:.0001pt\'>

bottom:.0001pt\'>Die gesamte Hamilton-Funktion folgt durch Integration über  und  und verschwindet ebenfalls. (Oberflächenterme, die im Falle asymptotisch flacher Raumzeiten auftauchen, seien hier unberücksichtigt.) Im Falle der Geometrodynamik lautet die explizite Form der klassischen Zwangsbedingungen

bottom:.0001pt\'>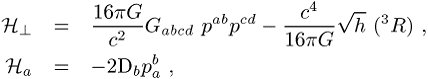

bottom:.0001pt\'>wobei  die Determinante der Metrik,  den dreidimensionalen Ricci-Skalar und  die kovariante Ableitung bezeichnen (eine mögliche kosmologische Konstante wurde nicht berücksichtigt).  ist die sogenannte DeWitt-Metrik; sie ist von indefiniter Natur.

bottom:.0001pt\'>In der Zusammenhangsdynamik hat man stattdessen

bottom:.0001pt\'>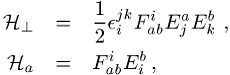

bottom:.0001pt\'>wobei  der zu  gehörende Feldstärketensor ist (analog zu Yang-Mills-Theorien). Hier gibt es zudem noch drei weitere Zwangsbedingungen, welche mit der Freiheit zu tun haben, das Dreibein  lokal zu drehen.

bottom:.0001pt\'>Die Quantisierung der kanonischen Theorie erfolgt nun, indem man im Schrödinger-Bild (Bilder in der Quantenmechanik) die Impulse  bzw.  durch die entsprechenden Ableitungen nach den Ortsvariablen  bzw.  ersetzt. Aus den klassischen Zwangsbedingungen werden dann (funktionale) Differentialoperatoren, die auf Wellenfunktionale  angewandt werden. Im Falle der Quantengeometrodynamik werden aus (1) und (2) somit

bottom:.0001pt\'>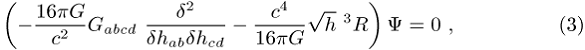

bottom:.0001pt\'>

bottom:.0001pt\'>Analoge Gleichungen folgen für die Quantenzusammenhangsdynamik. Solange die genaue Faktorordnung noch offen bleibt, ist der kinetische Term in (3) nur formal zu verstehen. Wegen (4) ist das Wellenfunktional unabhängig von der Wahl der Koordinaten, was gerne durch die symbolische Schreibweise  zum Ausdruck gebracht wird, wobei  für dreidimensionale Geometrie steht. Zusammengefasst haben diese Gleichungen die Form

bottom:.0001pt\'>

bottom:.0001pt\'>mit  als Hamilton-Operator. Diese Gleichung heisst auch Wheeler-DeWitt-Gleichung. In Tabelle 1 werden die wesentlichen Strukturen der Geometrodynamik den entsprechenden Strukturen der Mechanik gegenübergestellt.

bottom:.0001pt\'>An den Grundgleichungen der kanonischen Quantengravitation ist auffallend, dass sie keinen Zeitparameter mehr enthalten - (5) hat formal die Gestalt einer stationären Schrödinger-Gleichung zur Energie Null. Diese Tatsache wird oft als das Zeitproblem der Quantengravitation bezeichnet. Es besteht auch in der String-Theorie und ist von grundlegender Bedeutung für die Interpretation der Theorie.

bottom:.0001pt\'>Exakte Lösungen der vollen Wheeler-DeWitt-Gleichung konnten bisher nur in der Zusammenhangs- bzw. Schleifendarstellung gefunden werden. Dort ist es unter anderem gelungen, einen Flächenoperator zu definieren und nachzuweisen, dass dieser ein diskretes Spektrum besitzt. Aus diesem Grunde kommt beliebig kleinen Distanzen keine operationelle Bedeutung zu - die kleinste Distanz ist von der Ordnung der Planck-Länge.

bottom:.0001pt\'>In der Quantengeometrodynamik können exakte Lösungen gefunden werden, wenn man sich auf einfache Modelle beschränkt. In der Quantenkosmologie studiert man häufig den Fall, wo nur der Skalenfaktor (»Radius«) a des Universums und ein homogenes skalares Feld  quantisiert werden. Aus dem Wellenfunktional wird dann eine Wellenfunktion . Im einfachsten Fall ist die Wheeler-DeWitt-Gleichung von der Form eines indefiniten Oszillators:

bottom:.0001pt\'>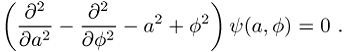

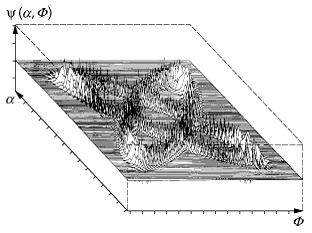
[21]Abb. 2 zeigt eine Lösung dieser Gleichung, welche der Superposition zweier Wellenpakete entspricht.

Aus der »zeitlosen« Gleichung (5) lässt sich im Rahmen einer semiklassischen Näherung die gewöhnliche (funktionale) Schrödinger-Gleichung für nichtgravitative Freiheitsgrade wiederfinden. Dabei taucht ein approximativer Zeitparameter auf, der durch die semiklassischen Freiheitsgrade definiert wird. Der Begriff der Raumzeit ist damit selbst ein semiklassischer Begriff. Höhere Ordnungen liefern dann Korrekturterme, die proportional zu G sind und Effekte der Quantengravitation beschreiben.

Anwendungsbereiche

In welchen Bereichen würde man beobachtbare Effekte der Quantengravitation erwarten? Experimentell zugänglich sind im Bereich Gravitation und Quantentheorie bisher nur Effekte, welche die Schrödinger-Gleichung in einem äusseren Gravitationspotential betreffen (Neutroneninterferometrie), worin freilich nur klassische Eigenschaften des Gravitationsfelds eingehen. Denkbare Anwendungsbereiche einer Quantengravitation wären die folgenden:

·        Quanteneffekte Schwarzer Löcher: Wegen des Hawking-Effektes geben Schwarze Löcher Strahlung von thermischer Natur ab. Die Temperatur ist dabei umgekehrt proportional zur Masse, so dass das Loch durch die Abstrahlung immer heisser wird und weiter an Masse verliert. Kommt die Masse in den Bereich der Planck-Masse, so verlieren die Annahmen, die in die Ableitung des Hawking-Effektes eingehen, ihre Gültigkeit. Nur eine Theorie der Quantengravitation kann vorhersagen, wie das Endstadium bei der Verdampfung Schwarzer Löcher abläuft. Um dies beobachten zu können, braucht man Schwarze Löcher von geringer Masse, da bei grosser Masse die Lebensdauer des Loches das Alter des Universums bei weitem übersteigt. Kleine Schwarze Löcher können nicht bei dem Kollaps gewöhnlicher Sterne entstehen, so dass sie schon beim Urknall entstanden sein müssen. Solche primordialen Schwarzen Löcher verraten sich beispielsweise durch ihre Gammastrahlung, nach der in einigen Projekten gesucht wird. Auch vor Erreichung des Endstadiums können sich Abweichungen vom thermischen Spektrum der Hawking-Strahlung ergeben, die sich aus einem diskreten Spektrum für die Masse des Loches in der Quantengravitation ergeben (was wiederum aus der diskreten Natur der Fläche folgt).

·        Kosmologie: Wenn die Vorstellungen über das inflationäre Universum stimmen, haben die im Spektrum der kosmischen Hintergrundstrahlung beobachteten Anisotropien ihren Ursprung in Quantenfluktuationen im frühen Universum. Da hierbei auch Quantenfluktuationen der Metrik eingehen, spielt die Quantengravitation eine Rolle. Denkbar ist etwa, dass Effekte beobachtbar sind, welche aus einer Entwicklung der Wheeler-DeWitt-Gleichung nach Potenzen von  resultieren. Auch die String-Theorie sagt Szenarien voraus, welche einen Einfluss auf dieses Spektrum haben könnten. Von ausserordentlicher Bedeutung wäre die Beobachtung eines Gravitationswellenhintergrundes, dessen Existenz im Rahmen dieser Vorstellungen vorhergesagt wird. Vorstellbar ist schliesslich auch, dass fundamentale Konstanten der Physik wie etwa die kosmologische Konstante aus fundamentalen Theorien der Quantengravitation abgeleitet werden können.

·        Raumzeit auf kleinsten Skalen: Wie oben erwähnt, sagen einige Zugänge zur kanonischen Quantengravitation ein diskretes Spektrum für die raumzeitlichen Abstandsverhältnisse voraus. Ähnliches gilt für die String-Theorie. Es existieren Vorschläge, wonach diese diskrete Natur zu beobachtbaren Effekten im Spektrum der Photonen führen, die als Gamma-Bursts (Burster) aus weitentfernten astrophysikalischen Quellen stammen.

Vermutlich wird die endgültige Theorie der Quantengravitation zudem Effekte hervorbringen, die sich der heutigen Vorstellungskraft noch entziehen.

 

Ausblick

Auch wenn eine allgemein akzeptierte Theorie der Quantengravitation noch aussteht, versteht man doch grundlegende Konzepte und Probleme, die bei ihrer Konstruktion eine Rolle spielen, und hat zudem mit String-Theorie und kanonischer Quantengravitation erfolgversprechende Modelle zur Hand. Von zentraler physikalischer Bedeutung sind die nichtstörungstheoretische Natur der Theorie und ihre Vorhersagen für die fundamentale Struktur von Raum und Zeit. Zu erwarten ist auch ein tieferes Verständnis der Quantentheorie allgemein. In ihrer Anwendung auf das Universum als Ganzes lässt sie keinen Raum mehr für äussere klassische Beobachter. Vielmehr müssen klassische Eigenschaften intrinsisch entstehen, wie es das Programm der Dekohärenz leistet. Die philosophischen Konsequenzen einer solchen Theorie sind bisher nicht einmal ansatzweise ausgelotet worden.

 

Literatur:

A. Ashtekar, Quantum mechanics of geometry. Preprint gr-qc/9901023.

J. Ehlers und H. Friedrich (Hg.), Canonical gravity: From classical to quantum, Springer, Berlin, 1994.

J.J. Halliwell, Introductory lectures on quantum cosmology. In: Quantum cosmology and baby universes, hg. von S. Coleman, J.B. Hartle, T. Piran und S. Weinberg, World Scientific, Singapore, 1991.

C.J. Isham, Canonical quantum gravity and the problem of time. In: Integrable Systems, Quantum Groups,  and Quantum Field Theories, hg. von L.A. Ibart und M.A. Rodrigues, Kluwer, Dordrecht, 1993.

C. Kiefer, Conceptual issues in quantum cosmology. In: From cosmology to quantum gravity, hg. von J. Kowalski-Glikman, Springer, Berlin, 1999.

K.V. Kucha, Time and interpretations of quantum gravity. In: Proceedings of the 4th Canadian Conference on General Relativity and Relativistic Astrophysics, hg. von G. Kunstatter, D. Vincent und J. Williams, World Scientific, Singapore, 1992.

J. Polchinski, Quantum mechanics at the Planck length. International Journal of Modern Physics A 14, 2633-2658 (1999).

S. Weinberg, Dreams of a final theory, Hutchinson Radius, London, 1993.

H.D. Zeh, The physical basis of the direction of time, Springer, Berlin, 1999.

 

Quantengravitation: Vergleich zwischen Mechanik und Geometrodynamik.