Techniklexikon

Metrik

Mathematische Methoden und Computereinsatz, 1) eine Abstandsfunktion  auf einer Menge  mit (a)  und , (b) , (c)  (Dreiecksungleichung).  heisst dann metrischer Raum. Beispiele dafür sind der  mit euklidischer Metrik  oder ein Hilbert-Raum  mit .

2) ein metrisches Feld; das ist ein symmetrisches kovariantes Tensorfeld

auf einer Mannigfaltigkeit , so dass die Matrix  für alle  invertierbar ist. Die Komponenten des durch Invertierung von  entstehenden kontravarianten Tensorfeldes  schreibt man mit oberen Indizes:

 Eine Metrik induziert einen Isomorphismus zwischen ko- und kontravarianten Tensoren (»Herauf- bzw. Herunterziehen« von Indizes): Einem Tangentenvektor  bei  wird die 1-Form (Differentialformen)  und einer 1-Form  bei  der Tangentenvektor  zugeordnet. In einem Kartenbereich (Mannigfaltigkeiten) gibt es ein orthonormales n-Bein,  (Tensorfelder) von 1-Formen , so dass 

  mit konstanter Diagonalmatrix  und  für  und  für . I.a. gibt es aber keine lokalen Koordinaten , so dass . Der Raum  heisst dann gekrümmt (Krümmung). Falls es aber solche lokalen Koordinaten gibt, heisst der Raum lokal flach und, falls man mit einem einzigen solchen Koordinatensystem auskommt, flach. Ein flacher Raum muss mit einem  übereinstimmen. Ist die Matrix  für alle x positiv definit, heisst g eine Riemannsche Metrik, sonst pseudo-Riemannsch.  nennt man dann einen Riemannschen bzw. pseudo-Riemannschen Raum. Im Riemannschen Fall kann man eine Orthonormalbasis so finden, dass  die Einheitsmatrix ist, und es lässt sich aus g eine Metrik im Sinne von (1) konstruieren.

In der Allgemeinen Relativitätstheorie repräsentiert eine pseudo-Riemannsche Metrik g auf der vierdimensionalen Raumzeit das Gravitationsfeld. Hier spielen die Christoffel-Symbole (Christoffel-Konnexion) einer Metrik g eine bedeutende Rolle. Sie sind relativ zu einem lokalen Koordinatensystem  definiert durch

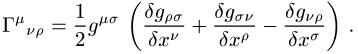
Sie bilden die Komponenten des Riemannsches Zusammenhanges. Die Geodäten von g sind die Kurven  in , die die Gleichung

 erfüllen. Sie verallgemeinern die gleichförmige kräftefreie Bewegung eines Teilchens im flachen Raum auf Bewegungen in gekrümmten Räumen. Interpretiert man g als Schwerefeld, so sind die Geodäten die möglichen Bahnkurven von Teilchen, die nur der Schwerkraft unterworfen sind.