Techniklexikon

Divergenz

Mathematische Methoden und ComputereinsatzOptikQuantenmechanikTeilchenphysik, 1) Feldtheorie: das einem dreidimensionalen Vektorfeld F(r) zugeordnete skalare Feld (div F)(r), das man durch Anwendung des Divergenzoperators aus diesem erhält. Die Divergenz spielt in der Elektrodynamik (Maxwell-Gleichungen) und in der Hydrodynamik eine wichtige Rolle. Für Vektorfelder und deren Divergenz gilt der Gausssche Satz , gemäss dem das Flächenintegral eines Vektorfeldes über eine geschlossene Fläche S gleich dem Volumenintegral der Divergenz dieses Feldes über das von S eingeschlossene Volumen V ist. Aus dem Gaussschen Satz ergibt sich eine anschauliche Deutung der Divergenz: Fasst man F(r)dA als "Ausströmung" aus V durch das Flächenelement dA auf, so muss die von S umschlossene Divergenz die "Quelle" dieser Strömung sein. Die Divergenz wird daher auch als Quelldichte bezeichnet. Orte mit positiver Divergenz heissen Quellen des Vektorfeldes, Orte mit negativer Divergenz heissen Senken. Ist die Divergenz überall Null, heisst das Vektorfeld divergenzfrei. Magnetfelder sind immer divergenzfrei. Zu einem divergenzfreien Feld F(r) lässt sich stets ein anderes Vektorfeld A(r) finden, für das rot A =  Ñ ´ F = F gilt (Rotation). Häufig schreibt man die Divergenz auch als Skalarprodukt div F = Ñ × F des Nabla-Operators Ñ mit dem Vektor F.

Die Divergenz div F lautet in kartesischen Koordinaten (x,y,z)

in Zylinderkoordinaten (r,f,z)

und in Kugelkoordinaten (r,q,f)

Für beliebige Vektorfelder A(r), B(r) und skalare Felder F(r) gelten ausserdem die Formeln

div (rot A)  = 0,

div (FA)_   = F(div A) + (gradF) ´ A,

div r_  = 3 und

div (A ´ B) = B rot A - A rot B.

Die Divergenz des Gradienten eines skalaren Feldes F ist der Laplace-Operator: DF : = div(grad F).

2) Mathematik: die Eigenschaft einer Folge, keinen Grenzwert zu besitzen, die Eigenschaft einer Reihe, nicht zu konvergieren, oder die Eigenschaft eines uneigentlichen Integrals, nicht zu existieren.

3) Optik: Bezeichnung für das Auseinanderlaufen von Lichtstrahlen, im Gegensatz zur Konvergenz (Zusammenlaufen von Strahlen).

4)^[n] Quantenfeldtheorie, Elementarteilchenphysik: die Bezeichnung für alle Arten von Unendlichkeiten, die bei der Berechnung physikalischer Observabler, z.B. Wirkungsquerschnitte, Zerfallsbreiten usw. auftreten. Man unterscheidet ultraviolette (UV), infrarote (IR) und kollineare Divergenzen sowie Coulomb-Singularitäten. Um mit divergenten Zwischenausdrücken sinnvoll umgehen zu können, müssen diese geeignet regularisiert werden (Regularisierung); summiert man alle Beiträge des vollen physikalischen Prozesses, so heben sich sämtliche IR-, kollinearen-, und Coulomb-Singularitäten gegenseitig weg. Die UV-Divergenzen werden durch die Renormierung beseitigt.

Kollineare und Infrarot-Divergenzen: Kollineare Divergenzen (sog. Massensingularitäten) treten nur in Feynman-Diagrammen mit masselosen äusseren Teilchen auf, und zwar genau dann, wenn sich zwei masselose ein- oder auslaufende Teilchen mit Impulsen p₁, p₂ parallel zueinander bewegen, also für die Viererimpulse  gilt. IR-Divergenzen können in Diagrammen mit geschlossenen Schleifen auftreten, bei denen mindestens ein Teilchen in der Schleife masselos ist, oder in Bremsstrahlungsdiagrammen mit masselosen abgestrahlten Teilchen. Die IR- und kollinearen Divergenzen werden durch die Hinzunahme der Beiträge mit der zusätzlichen Abstrahlung eines "weichen" masselosen Teilchens kompensiert. Physikalisch ist diese Vorgehensweise gerechtfertigt, da man im Detektor die zusätzlichen Beiträge experimentell nicht vom eigentlich interessierenden Prozess trennen kann.

Die Coulomb-Singularität tritt in Fällen auf, in denen zwei Teilchen "in Ruhe" produziert werden, d.h. wenn die Relativgeschwindigkeit  geht. Sie stellt einen nichtstörungstheoretischen Effekt dar und modifiziert das - anziehende oder abstossende - Potential zwischen den beiden Teilchen. In der Praxis werden die 1/v-Singularitäten in der Wellenfunktion am Ursprung  absorbiert.

UV-Divergenzen treten bei der Berechnung von Feynman-Diagrammen auf, die zu Strahlungskorrekturen höherer Ordnung (Schleifen-Diagramme, engl. loop diagrams) gehören. Die

entsprechenden Integrale vom Typ

(p ist der Schleifen-Impuls, über den integriert wird, Abb.) divergieren für  (ultravioletter Bereich). Der Grad D der Divergenz eines Feynman-Diagramms bzw. seines entsprechenden Integrals lässt sich für grosse Impulse p durch einfaches Abzählen der Potenzen von p ermitteln (power counting). Jeder Boson-Propagator trägt p ^{- 2} und jeder Fermionpropagator p ^{- 1} bei, jede Schleife eine Integration mit p⁴ und jeder Vertex mit n Ableitungen höchstens pⁿ. Das Integral wird divergent, wenn die Gesamtpotenz von p, der sog. Divergenzgrad D, gleich oder grösser Null ist. Zur Verdeutlichung soll das Beispiel der Quantenelektrodynamik dienen: jedes Diagramm der QED besteht aus einer bestimmten Anzahl innerer (I_y) und äusserer (E_y) Elektronlinien sowie I_A inneren und E_A äusseren Photonlinien; es enthält L Schleifen und V Vertizes. Dann beträgt der Divergenzgrad

D = 4L - 2I_A - I_y.

Er kann auch als Funktion nur der äusseren Linien geschrieben werden,

,

d.h. der Divergenzgrad in der QED ist unabhängig von der unter Umständen komplizierten Struktur der inneren Linien. Man rechnet leicht nach, dass die Selbstenergie des Elektrons den Divergenzgrad D = 1, die Selbstenergie des Photons hingegen
D = 2 aufweist.

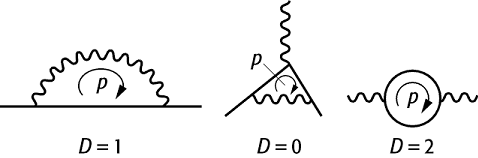
Divergenz: Bei der Berechnung von Strahlungskorrekturen, z.B. in der Quantenelektrodynamik, führt die Integration über den inneren Impuls p zu unendlichen Beiträgen. Links die Elektron-Selbstenergie (Divergenzgrad D = 1), in der Mitte der Elektron-Photon-Vertex (D = 0), rechts die Photon-Selbstenergie (D = 2).