Techniklexikon

Lorentz-Gruppe

Mathematische Methoden und Computereinsatz, homogene Lorentz-Gruppe, die Gruppe L aller -Matrizen , die den verallgemeinerten Abstand zweier Raumzeitpunkte (Weltpunkte),

invariant lassen (Lorentz-Transformation). Sie zerfällt in vier Zweige aufgrund der Eigenschaften  (also  oder ) und  (also  oder ) der Lorentz-Transformationen:

1)  (), dazu zählen die Identität E, die Drehungen und die speziellen Lorentz-Transformationen (Lorentz-Boosts);

2)  (), dazu zählen das Produkt PT aus Spiegelung P und Zeitumkehr T sowie alle  mit ;

3) , dazu zählen P sowie alle  mit ;

4) , dazu zählen T sowie alle  mit .

Nur der Zweig  bildet eine Untergruppe der Lorentz-Gruppe, die eigentliche, ortochrone Lorentz-Gruppe, die anderen Zweige nicht.

Die Lorentz-Gruppe hat sechs Parameter; ihre infinitesimalen Erzeugenden  erfüllen die Vertauschungsrelationen

In der Darstellung mit -Matrizen können sie geschrieben werden als ()

Definiert man , erhält man

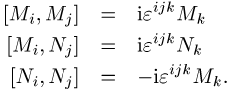
Die endlich-dimensionalen und nicht-unitären irreduziblen Darstellungen der eigentlichen, orthochronen Lorentzgruppe (genauer: der sie überdeckenden Gruppe SL(2,C)) werden durch zwei nicht-negative ganzzahlige (Tensor-Darstellungen) oder halbzahlige (Spinordarstellungen) Labels  gekennzeichnet und haben die Dimension . Die unendlich-dimensionalen und unitären irreduziblen Darstellungen sind durch zwei Zahlen (c, M) gekennzeichnet mit der Eigenschaft:

1) c ist eine beliebige imaginäre Zahl und M eine beliebige nicht-negative Zahl (ganz- oder halbzahlig);

2) c ist eine reelle Zahl mit  und M = 0.