Techniklexikon

Drehimpulsoperator

 ist ein Drehimpulsoperator, der auf das erste,  ein Drehimpulsoperator, der auf das zweite Teilchen wirkt. Es gilt . Die Quantenzahlen der jeweiligen Teilchen addieren sich dabei zu der Gesamtdrehimpuls-Quantenzahl, zum Beispiel

Der Darstellungsraum  ist jedoch reduzibel und zerfällt in folgende irreduziblen Unterräume:

Das bedeutet, dass sich zwei Teilchen mit dem jeweiligen Betrag des Drehimpulses j₁ und j₂ nur zu Drehimpulsen des Betrages j₁ + j₂, j₁ + j₂ - 1,..., |j₁ - j₂| addieren können. Man kann eine Basis  des Zweiteilchen-Hilbert-Raumes einführen, wobei J = j₁ + j₂ und M = m₁ + m₂. Führt man für die Basis  die Schreibweise  ein, so kann man  wie folgt entwickeln: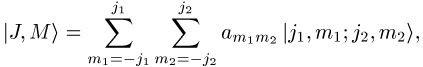

wobei die Entwicklungskoeffizienten durch  gegeben sind. Man nennt die Entwicklungskoeffizienten  auch Clebsch-Gordan-Koeffizienten. Die Wahl der jeweiligen Basis hängt von dem zu beschreibenden Problem ab. So kann sich zum Beispiel beim Paschen-Back-Effekt die Wahl der Basis  als ungeeignet erweisen.

Koppelt man mehr als zwei Drehimpulseigenvektoren, so kann man dies durch Hintereinanderausführen von paarweisen Kopplungen erreichen, wobei man schon ab drei Drehimpulseigenvektoren mehrere Möglichkeiten der Kopplung besitzt. Betrachtet man zum Beispiel drei Drehimpulseigenvektoren  und die Basis des gekoppelten Raumes , so kann man zuerst die ersten beiden Drehimpulseigenvektoren zusammenfassen, , um danach die verbleibenden Eigenvektoren zu dem Gesamtdrehimpuls J zu koppeln, , oder man fasst zuerst die letzten beiden Eigenvektoren zusammen und koppelt dann die verbleibenden Eigenvektoren, was mit  bezeichnet werden soll. Diese Gesamtdrehimpulseigenfunktionen werden durch folgende unitäre Transformation ineinander übergeführt:

Die Entwicklungskoeffizienten W bezeichnet man als Racah-Koeffizienten.