Techniklexikon

Levi-Civita-Symbol

auch Permutationssymbol genannt, ein dreifach indiziertes Objekt, das der folgenden Definition genügt:

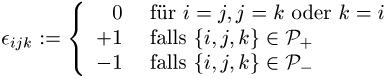
mit

Das Levi-Civita-Symbol genügt den Bedingungen

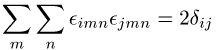
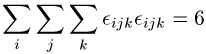
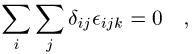
wobei  das Kronecker-Symbol ist. Das Levi-Civita-Symbol kann auch mit Hilfe des Skalar- und Kreuzproduktes durch die drei Einheitsvektoren e_i eines rechtshändigen kartesischen Koordinatensystems ausgedrückt werden: . Je nachdem, ob im dreidimensionalen Raum die Vektoren e₁, e₂ und e₃ in Abhängigkeit von ihrer Permutation ein positives oder negatives Koordinatensystem aufspannen, hat  den Wert +1 oder -1. Desweiteren kann das Levi-Civita-Symbol auch als dreifach indizierter Tensor interpretiert werden; in diesem Falle wird es auch Levi-Civita-Tensor oder Permutationstensor genannt.