Techniklexikon

Inertialsystem

Navigation /Trägheitsnavigation Bezugssystem, in dem Körper sich gemäss den Newtonschen Axiomen bewegen, in dem also keine Scheinkräfte, wie beispielsweise Fliehkräfte, auftreten. Bezugssysteme, die sich gegenüber einem Inertialsystem gleichförmig bewegen, sind ebenfalls Inertialsysteme. Da in der Newtonschen Physik Raum und Zeit geometrisch sehr unterschiedlich behandelt werden, ist eine rein geometrische Definition eines Inertialsystems auf dieser Basis nicht möglich. In der Minkowski-Raumzeit, die der Speziellen Relativitätstheorie zugrunde liegt, bzw. in noch allgemeineren Raumzeiten, lässt sich hingegen ein Inertialsystem kartesischer Koordinaten definieren als ein System, in dem der metrische Tensor (Metrik) die Form

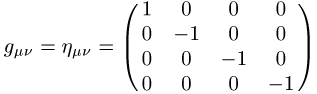
hat. Alle anderen Inertialsysteme gehen aus ihm hervor, indem man die Zeit-Koordinate festhält und die Raum-Koordinaten zeitunabhängig transformiert.

In der Praxis verwendete Bezugssysteme sind stets nur näherungsweise Inertialsysteme. Insbesondere ist ein übliches Laborsystem aufgrund der Schwerkraft und der Erdrotation kein Inertialsystem. Der Übergang von der Beschreibung der Physik in Inertialsystemen zu einer allgemein gültigen physikalischen Theorie entspricht dem Übergang von der Newtonschen Mechanik bzw. der Speziellen Relativitätstheorie zur Allgemeinen Relativitätstheorie.