Techniklexikon

Darstellung einer Gruppe

Zuordnung einer nichtsingulären linearen Abbildung in einem Vektorraum M zu jedem Element g einer Gruppe. Nach Festlegung einer Basis des Vektorraums, der auch als Darstellungsraum bezeichnet wird, ist die Darstellung einer Gruppe G dadurch definiert, dass jedem Gruppenelement g Î G eine nichtsinguläre Matrix D(g) in solcher Weise zugeordnet ist, dass die Multiplikationsregel der Gruppe beibehalten wird, also  gilt. Die Dimension m des Darstellungsraumes heisst Grad der Darstellung.

Die Theorie der Darstellungen von Gruppen ist, wie die Gruppentheorie allgemein, in der Physik von grösster Bedeutung bei der Beschreibung von Symmetrien der betrachteten Systeme, aus denen sich oft weitreichende Schlüsse auf die Gestalt der Lösungen ziehen bzw. wichtige Erhaltungssätze ableiten lassen. Zum Beispiel folgt der Satz von der Erhaltung der Energie aus der Annahme, dass physikalische Gesetze zu jedem Zeitpunkt dieselben sein sollten, also invariant gegen die Symmetrietransformation Zeitverschiebung; und die Erhaltung der elektrischen Ladung ergibt sich aus einer Symmetrieeigenschaft der Wellenfunktionen, mit denen Elementarteilchen in der Quantenmechanik beschrieben werden. Die Gesamtheit der Symmetrietransformationen eines bestimmten Typs bilden oft eine Gruppe, deren Darstellungen die Struktur der Gruppe wiedergeben und deren Untersuchung allgemeine Aussagen bezüglich des spezifischen physikalischen Systems, das man betrachtet, erlaubt.

Hat der Raum einer Darstellung vom Grade n einen echten invarianten r-dimensionalen Unterraum V^(r), 0  < r  < n, so dass die durch D(g) abgebildeten Vektoren von V^(r) wieder in V^(r) liegen, so nennt man die Darstellung reduzibel; eine solche Darstellung kann in der Form

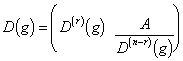
geschrieben werden. Ist auch noch A = 0, so hat man in dem zu V^(r) komplementären Unterraum V^{(n - r)} eine weitere Darstellung von G. Man sagt dann, dass die Darstellung D in die beiden Darstellungen D^(r)(G) und D^{(n - r)}(G) "zerfällt", und schreibt

.

Zerfallen nun die Darstellungen D^(r)(G), D^{(n - r)}(G) selbst wieder in reduzible oder irreduzible Darstellungen von G, so kann man das Verfahren fortsetzen, bis nur irreduzible Darstellungen D_k(G) übrigbleiben:

.

Man hat D damit "ausreduziert" und sagt, dass D vollständig reduzibel sei (ist , so ist D nicht vollständig reduzibel). In diesem Fall nimmt D Diagonalgestalt an. Bei der Darstellung einer Gruppe durch unitäre Abbildungen ist jede reduzible Darstellung zugleich vollständig reduzibel.

Kennt man also alle irreduziblen Darstellungen einer Gruppe, so kann man alle vollständig reduziblen aus ihnen aufbauen. Die irreduziblen Darstellungen einer Gruppe sind also die Grundbausteine der zugehörigen Darstellungstheorie, und darin liegt ihre grosse Bedeutung.

Ein wichtiges Kriterium für die Irreduzibilität einer Darstellung ist das Schursche Lemma: Ist das System aller darstellenden Matrizen einer bestimmten Darstellung der betrachteten Gruppe irreduzibel, so ist jede Matrix, die mit allen diesen Matrizen vertauscht, notwendig ein Vielfaches der Einheitsmatrix.

Von zentraler Bedeutung für die Quantentheorie, insbesondere für die Eichtheorien, sind die bereits erwähnten unitären Darstellungen von Gruppen, bei denen für je zwei beliebige Vektoren j, y des Darstellungsraums ein Skalarprodukt  definiert ist, das folgende Eigenschaft aufweist: Sind  die Bildvektoren von j und y, wenn man diese der dem beliebigen Gruppenelement a zugeordneten linearen Transformation U(a) unterwirft, so gilt

Die Bedeutung solcher unitären Darstellungen von Gruppen für die Quantentheorie liegt darin, dass man die zugehörigen Darstellungsräume als quantentheoretische Zustandsräume interpretieren kann, in denen  und  die physikalischen Zustände beschreiben, falls das System die entsprechenden Symmetrien erfüllt.

Eine grosse Zahl der physikalisch relevanten Gruppen gehört zu den Lie-Gruppen, z.B. die Drehgruppe, die Lorentz-Gruppe und die für die Elementarteilchenphysik enorm wichtigen SU(N)-Gruppen, zu denen u.a. die Eichgruppe der starken Wechselwirkung SU(3) gehören. Jedes Element g einer n-dimensionalen Lie-Gruppe aus der Umgebung des Einheitselements e lässt sich in der Form

parametrisieren, wobei die l_i die Erzeugenden der Gruppe (auch Generatoren genannt) sind, denen durch eine Darstellung D entsprechende Erzeugenden der Darstellung L_i zugeordnet werden, die eine Lie-Algebra aufspannen und die Kommutatorregeln

erfüllen, wobei die Strukturkonstanten c_ijk die jeweilige Lie-Algebra und damit auch die Gruppe selbst spezifizieren.

Mit Hilfe der Algebra lassen sich sämtliche Darstellungen einer Lie-Gruppe gewinnen. Ausgangspunkt bildet die Cartan-Subalgebra der Algebra. Sie besteht aus r miteinander vertauschenden Erzeugenden H_i (d.h. [H_i, H_j] = 0), die simultan diagonalisiert werden können; die entsprechenden Eigenvektoren lassen sich also durch r Eigenwerte kennzeichnen:

;

die Zahl r wird der Rang der Gruppe genannt. Die Eigenwerte können auch halbzahlig sein, man spricht dann von Spinor-Darstellungen (Lorentz-Gruppe).

Die Cartan-Subalgebra wird durch n - r Elementen E_a (engl. roots) mit der Eigenschaft [H_i, E_a] = a_i × E_a, d.h. E_a ist Eigenvektor von H_i mit Eigenwert a_i, zu einer vollständigen Basis der ganzen Algebra, der Cartan-Basis, ergänzt. Die E_a wirken als Leiteroperatoren, d.h. sie verändern die Eigenwerte eines Eigenvektors:

Die achtdimensionale Gruppe SU(3) beispielsweise, die aus allen komplexen unitären 3 ´> 3-Matrizen U mit der Eigenschaft det U = 1 besteht, wird von den acht Gell-Mann-Matrizen l_i erzeugt, von denen zwei, l₃ und l₈, diagonal sind und somit vertauschen; SU(3) hat also den Rang 2. Die Leiteroperatoren sind .

Durch sukzessive Anwendung der Leiteroperatoren auf den Zustand mit den höchsten Eigenwerten kann man jede Darstellung konstruieren; man erhält so in systematische Weise alle möglichen Darstellungen jeder Lie-Gruppe. Eine Sonderstellung nehmen die sogenannten fundamentalen irreduziblen Darstellungen, von denen jede Lie-Gruppe r besitzt und die mit  bezeichnet werden, wobei die 1 an der i-ten Stelle steht und i von 1 bis r läuft. SU(3) hat also zwei fundamentale irreduzible Darstellungen D(1,0) und D(0,1), die auch oft als 3 und  notiert werden.

Jede Darstellung von SU(N) lässt sich durch Tensorprodukte der fundamentalen Darstellungen gewinnen. Die Elemente des Darstellungsraumes dieser Tensordarstellungen sind Tensoren mit bestimmten Symmetrieeigenschaften, die sich besonders gut im Formalismus der Young-Diagramme (engl. Young tableaus) darstellen lassen. Er erlaubt es zudem, die explizite Form der Vektoren eines Darstellungsraumes zu ermitteln und die Reduzierung von Darstellungsprodukten in irreduzible Darstellungen durchzuführen. [UK]