Techniklexikon

Atomtheorie

theoretische Beschreibung der Elektronenstruktur der Atome (Atomhülle). Als erste quantitativ ausgearbeitete Atomtheorie kann die Bohrsche Theorie gelten, die zwar die spektroskopischen Eigenschaften von Einelektronenatomen im wesentlichen korrekt beschreibt, in deren Rahmen aber weder die Stabilität der Atome noch die Eigenschaften von Mehrelektronenatomen verstanden werden können. Dies ist erst auf der Basis der Quantenmechanik möglich, so dass man die Atomtheorie heute mit der Anwendung der Quantenmechanik auf die Beschreibung der Atomhülle identifizieren kann.

Die Atomtheorie gliedert sich in drei grosse Bereiche, nämlich die Eigenschaften freier Atome, die der Gegenstand des vorliegenden Beitrags sind, die Wechselwirkung von Atomen mit äusseren, meist elektromagnetischen Feldern und die Streuung vorwiegend geladener Teilchen an Atomen. Eine vollständige Theorie freier Atome muss die folgenden Wechselwirkungen umfassen:

(i) die kinetische Energie der Elektronen;

(ii) die potentielle Energie der Elektronen im Coulomb-Feld des als Punktladung angenommenen Atomkerns;

(iii) die elektrostatische Coulomb-Wechselwirkung der Elektronen;

(iv) relativistische Korrekturen;

(v) Strahlungskorrekturen (Quantenelektrodynamik, Lamb-Verschiebung);

(vi) Wechselwirkungen der Elektronen mit den Freiheitsgraden des Atomkerns (Hyperfeinwechselwirkungen).

Die Wechselwirkungen (i)-(iii) beschreiben die Grobstruktur der Atomspektren und erfassen zumindest für die leichten Atomen (etwa bis Argon) die wesentlichen Eigenschaften. Die relativistischen Korrekturen führen zur Feinstruktur der Atomspektren und umfassen bei einer Störungsrechnung erster Ordnung in ²/c² die Spin-Bahn- und Spin-Spin-Wechselwirkungen, eine Korrektur zur kinetischen Energie und den Darwin-Term. Der grösste Beitrag ist in der Regel die Wechselwirkung zwischen Bahnmoment und Spin desselben Elektrons; dieser Term ist in den meisten Fällen gemeint, wenn von Spin-Bahn-Kopplung gesprochen wird. Für die schwersten Atome (etwa ab Rubidium) werden die relativistischen Effekte so gross, dass die Beiträge erster Ordnung oft nicht mehr ausreichen oder eine Störungsrechnung überhaupt nicht mehr anwendbar ist. Die Berücksichtigung der endlichen Masse und Ausdehnung des Kerns sowie der Wechselwirkung der Elektronen mit den elektrischen und magnetischen Kernmomenten führt schliesslich zur Hyperfeinstruktur.

Das einzige analytisch lösbare atomare System ist das Wasserstoffatom (bzw. die wasserstoffartigen Ionen He ⁺ , Li ^{+  +}  usw.), das innerhalb der Atomtheorie eine paradigmatische Rolle insofern spielt, als sich die Konzeption der verschiedenen Näherungstheorien (Zentralfeldnäherung) für die Behandlung von Mehrelektronenatomen an den Ergebnissen für das Wasserstoffatom orientiert. Von zentraler Bedeutung ist dabei die aus der sphärischen Symmetrie und der Spinunabhängigkeit des Kern-Coulomb-Potentials folgende Faktorisierung der Atomorbitale in einen Radialteil R_nl(r), einen winkelabhängigen Anteil  (Kugelfunktionen) und einen spinabhängigen Anteil :

, (1)

wobei  ist. Im Fall des Wasserstoffatoms liefert diese Faktorisierung die exakte Lösung (solange nur die Grobstruktur berücksichtigt wird), während sie in Mehrelektronenatomen nur eine Näherungslösung ergibt.

Die theoretische Behandlung der Mehrelektronenatome muss als zusätzliche Faktoren die Wechselwirkung der Elektronen untereinander sowie ihre Ununterscheidbarkeit berücksichtigen. Die Schrödinger-Gleichung für dieses Problem, die im ersten Schritt nur die die Grobstruktur bestimmenden Wechselwirkungen (i)-(iii) enthält, lautet in atomaren Einheiten:

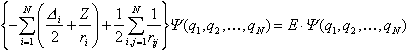, (2)

wobei die Wellenfunktion Y eine vollständig antisymmetrische Funktion der Elektronenkoordinaten q_i = (r_i,s_i) ist, d.h. bei Vertauschung je zweier Koordinaten das Vorzeichen ändert (Pauli-Prinzip). Während die Elektron-Elektron-Wechselwirkung eine analytische Lösung von Gl. 2) unmöglich macht, liefert die Ununterscheidbarkeit der Elektronen klassisch nicht mehr interpretierbare Beiträge zur elektronischen Gesamtenergie E, die pauschal als Austauschkorrelationsenergie bezeichnet werden. Für das Studium dieser Effekte spielt das Heliumatom (bzw. die Ionen mit zwei Elektronen) eine vergleichbar paradigmatische Rolle wie das Wasserstoffatom für Einelektronensysteme, weil hier Näherungsverfahren angewendet werden können, die für schwerere Atome nicht mehr praktikabel sind.

Die heute zumeist angewandte Strategie zur Lösung des Mehrelektronenproblems beginnt mit der Einteilchennäherung; hier wird entweder die Wellenfunktion durch Produkte von Atomorbitalen dargestellt (Hartree-Fock-Näherung) oder ein effektiver Einteilchen-Hamilton-Operator zu vorgegebener Einelektronendichte konstruiert (Lokale-Dichte-Näherung). Im ersten Fall muss der Ununterscheidbarkeit der Elektronen bzw. der Antisymmetrie der Wellenfunktion durch eine Darstellung als Slater-Determinante Rechnung getragen werden:

Zusammen mit Gleichung (2) führt dieser Ansatz auf die Hartree-Fock-Gleichung für das i-te Atomorbital:

,

die im Vergleich zu einer quasiklassischen Behandlung (Hartree-Näherung) als zusätzlichen Beitrag zur Gesamtenergie die Austauschenergie mit der nichtlokalen Hartree-Fock-Austauschladungsdichte  (Hartree-Fock-Näherung) enthält. In dieser Näherung bewegt sich jedes Elektron in einem effektiven Potential, das sich aus dem Kernpotential und der gemittelten (abstossenden) Wechselwirkung mit den übrigen N - 1 Elektronen zusammensetzt. Die Lösung der Hartree-Fock-Gleichung erfolgt nach dem Self-Consistent-Field-Verfahren und wird oft mit einer zusätzlichen sphärischen Mittelung der von der Elektron-Elektron-Wechselwirkung herrührenden Beiträge kombiniert (Zentralfeldnäherung). Die im Rahmen der Hartree-Fock-Näherung vernachlässigte Korrelation zwischen Elektronen mit entgegengesetztem Spin lässt sich durch störungstheoretische Methoden oder die Entwicklung der Wellenfunktion in Gl. 2) nach Slater-Determinanten für angeregte Zustände berücksichtigen (Vielteilchenmethoden).

Bei der zweiten Lösungsvariante, die Gegenstand der Dichtefunktionaltheorie ist, wird das atomare Mehrelektronenproblem durch einen in gewisser Weise komplementären Ansatz behandelt. Statt von einem vorgegebenen Hamilton-Operator entsprechend Gl. 2) auszugehen und die Vielteilcheneffekte über eine sukzessive Verbesserung der Wellenfunktion zu erfassen, versucht man hier, einen effektiven Hamilton-Operator zu konstruieren, der als Funktional der Einelektronendichte dargestellt wird. Der Einteilchennäherung entspricht hier die Lokale-Dichte-Näherung, in welcher die Gesamtenergie durch ein lokales Funktional der Einelektronendichte n(r) dargestellt wird, und in Orbitaldarstellung erhält man statt der Hartree-Fock-Gleichungen die Kohn-Sham-Gleichungen

mit dem lokalen Austausch-Korrelations-Potential _xc(n). Die Vielteilcheneffekte werden durch nichtlokale Austausch-Korrelations-Funktionale erfasst, deren Konstruktion eine der zentralen Aufgaben der Dichtefunktionaltheorie ist. Die theoretische Behandlung der Atome stellt heute selbst unter Berücksichtigung relativistischer Effekte kein Problem mehr dar und liefert Ergebnisse, die in vielen Fällen in präziser quantitativer Übereinstimmung mit experimentellen Daten stehen.[MG1]