Techniklexikon

Supergravitation

Relativitätstheorie und Gravitation, supersymmetrische Theorie der Gravitation, welche die Allgemeine Relativitätstheorie umfasst. Theorien der Supergravitation wurden zum ersten Mal 1976 von Freedman, van Nieuwenhuizen und Ferrara sowie Deser und Zumino diskutiert. Ausgangspunkt ist die Algebra der (globalen) Supersymmetrie mit Erzeugenden , die zwischen Bosonen und Fermionen vermitteln, sowie den Erzeugenden  und  der Poincaré-Gruppe. Neben der üblichen Algebra der Poincaré-Gruppe und der Translationsinvarianz der  spielt die Antikommutatorbeziehung

eine zentrale Rolle, wobei  die Dirac-Matrizen sind (). Fermionen und Bosonen werden durch irreduzible Darstellungen dieser Algebra in Supermultipletts vereinigt. Wünscht man die Transformationen der Supersymmetrie an jedem Raumzeitpunkt unabhängig durchzuführen, so muss man die Symmetrie eichen (Eichtheorien). Aus (1) folgt, dass dann Translationen (von  erzeugt) an jedem Punkt unabhängig vorgenommen werden können, was gerade die Durchführung allgemeiner Koordinatentransformationen ermöglicht. Deshalb enthält die durch die Eichung entstehende Supergravitation die Allgemeine Relativitätstheorie, genauer: die Einstein-Cartan-Theorie, welche durch die Eichung der Poincaré-Gruppe entsteht und neben der Krümmung zu einer Torsion für die Raumzeit führt. Mit den Erzeugern , ,  der Algebra sind die Eichfelder  (Vierbeinfeld),  (Zusammenhang),  (Rarita-Schwinger-Feld) verknüpft. Die Felder  haben Spin 3 / 2 und werden als Gravitinos bezeichnet. Im Falle N = 1 (einfache Supergravitation) gibt es ein Gravitino, das sich mit dem Graviton, das Spin 2 aufweist, ein Multiplett teilt. Gravitinos sind zunächst masselos, erhalten aber eine Masse durch den Higgs-Mechanismus (spontane Symmetriebrechung).

Bei  spricht man von erweiterter Supergravitation. Für  sind zwei Gravitinos, ein Graviton und ein Photon in einem Multiplett vereinigt, was eine vereinheitlichte Theorie von Gravitation und Elektromagnetismus ergibt. Fordert man, dass es nur ein Graviton gibt und dass keine Spins grösser als 2 auftauchen, so gilt (in 4 Raumzeitdimensionen) . (Für Spins grösser als 2 kennt man keine befriedigende Kopplung an andere Felder.) Im Falle N = 1 ist die Wirkung der Supergravitation die Summe aus Einstein-Hilbert-Wirkung und Rarita-Schwinger-Wirkung für das Gravitino:

wobei die spinorielle kovariante Ableitung durch den Ausdruck

gegeben ist. Die Wirkung (2) ist nicht nur invariant unter allgemeinen Koordinatentransformationen und lokalen Poincaré-Transformationen, sondern auch unter lokalen Supersymmetrietransformationen, die für Vierbein und Gravitinofeld lauten:

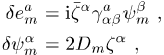
mit  als antikommutierender infinitesimaler Parameterfunktion. Man kann vierdimensionale Wirkungen auch aus höherdimensionalen -Theorien gewinnen, indem man eine Reduktion wie in Kaluza-Klein-Theorien vornimmt. Interessant ist dabei insbesondere die Supergravitation in 11 Raumzeitdimensionen, da dies die höchstmögliche Dimension für Supergravitationstheorien darstellt (dort ist nur N = 1 erlaubt) und bedeutsam für die Stringtheorie ist.

Theorien der Supergravitation lassen sich auch in einem »Superraum« beschreiben (der nichts mit dem Superraum der kanonischen Quantengravitation zu tun hat), bei dem die gewöhnlichen Raumzeitkoordinaten  durch antikommutierende Koordinaten  ergänzt werden, für welche die  Translationen erzeugen.

Da Quantenfeldtheorien der Gravitation wegen der dimensionsbehafteten Kopplungskonstanten ( in D Raumzeitdimensionen) i.a. nicht renormierbar sind (Quantengravitation), können Divergenzen in einzelnen Ordnungen der Störungstheorie nur unter besonderen Umständen (z.B. wegen des Vorhandenseins von Symmetrien) verschwinden. Für D = 4 verschwindet die Divergenz bei einer Schleife nach einer Umdefinition der Felder wie bei der reinen Gravitation ohne Gravitino. Wegen der Supersymmetrie gibt es keinen 2-Schleifen-Term, jedoch treten für N < 8 in 3 Schleifen Divergenzen auf (für N = 8 scheint dies nicht der Fall zu sein, weshalb dort Probleme erst ab 5 Schleifen erwartet werden). Für D = 11 gibt es schon ab 2 Schleifen Divergenzen. Die störungstheoretische Nichtrenormierbarkeit der Quantengravitation tritt also auch bei der Supergravitation auf. Aus diesem Grund ist für eine konsistente Quantentheorie der Gravitation eine ab initio nichtstörungstheoretische Formulierung (Quantengravitation) oder eine Aufgabe des Feldbegriffs auf fundamentaler Ebene (Stringtheorie) vorzunehmen.

Für das Gravitino erwartet man nach der Symmetriebrechung eine Masse von der Grössenordnung 100 GeV. Das könnte zu Problemen in der Kosmologie führen, da erzeugte Gravitinos eventuell eine überkritische Dichte des Universums bewirken. Hieraus ergeben sich starke Einschränkungen an inflationäre kosmologische Modelle (Inflation), die auf Supergravitation basieren.