Techniklexikon

kosmologische Modelle

Relativitätstheorie und Gravitation, Weltmodelle, Lösungen der Einstein-Gleichungen, die die Entwicklung des Kosmos beschreiben. Die aus der Hintergrundstrahlung erschlossene Gleichförmigkeit der Welt zusammen mit der allgemeinen Expansion legen einfache homogen-isotrope Modelle nahe, die sog. Friedmann-Lemaître (FL)-Modelle (nach Friedmann (1922) und Lemaître (1927), die zum ersten Mal Lösungen aus Einsteins Gravitationstheorie abgeleitet haben). Jedes dieser Friedmann-Lemaître-Modelle ist durch die Werte einiger weniger, im Prinzip messbarer, Parameter, wie die jetzige Ausdehnungsgeschwindigkeit des Galaxiensystems, die mittlere Dichte, die Temperatur des kosmischen Strahlungsfeldes charakterisiert. Die Expansion wird als das Auseinanderfliessen einer idealisierten, gleichmässig verteilten Materie aufgefasst, die durch homogene Dichte  und Druck  beschrieben wird. Die Flüssigkeitsteilchen, die man sich in diesem Bild als repräsentativ für die Galaxien denken kann, schwimmen in der sich ausdehnenden kosmischen Materie; ihr Abstand vergrössert sich mit der Zeit, proportional zum Expansionsfaktor . Das Linienelement wird zu , wobei  das Linienelement des Raumes mit konstanter Krümmung  ist. Dabei lassen sich die Massstäbe so wählen, dass  (sphärisch), 0 (flach),  (hyperbolisch) ist. Für R ergeben sich aus den Einstein-Gleichungen die Differentialgleichungen

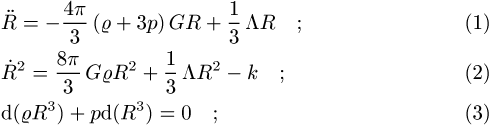
 ist die Gravitationskonstante,  die Krümmung, ,  Dichte und Druck.  ist eine Konstante, die von Einstein zunächst eingeführt wurde, um eine statische Lösung zu erzwingen, später aber von ihm stets null gesetzt wurde (kosmologische Konstante). Man kann sie ganz pragmatisch als einen Parameter betrachten, der evtl. durch Beobachtungen bestimmt werden muss. Falls , folgt aus je zwei der Gleichungen (1) bis (3) die dritte. Die Dynamik des kosmologischen Modells ist bestimmt, falls  oder ähnliche Zustandsgleichungen gegeben sind.

Zur gegenwärtigen Zeit  und für  kann man die Gleichungen (1) und (2) mit der Definition der Hubble-Konstanten  ( etc.) und des Akzelerationsparameters  umschreiben in die algebraischen Beziehungen

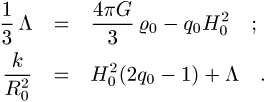
Es ist vorteilhaft, einen Dichteparameter einzuführen:

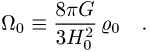
Entsprechend ersetzt man  durch eine Grösse :

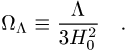
Diese Schreibweise macht deutlich, dass es nur eine Skala in den FL-Modellen gibt, nämlich die Hubble-Konstante . Alle anderen Grössen können als dimensionslose Verhältniszahlen dargestellt werden. Das Vorzeichen von  ist durch  bestimmt:

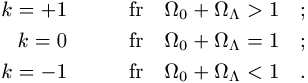
Falls man nun Gleichung (2) ebenfalls in diesen Termen aufschreibt und dazu die Beziehung  (folgt aus (3) für ) benutzt, so findet man

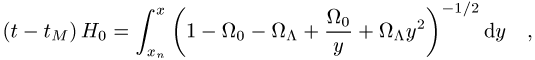
wobei  und  eine Zeit in der Vergangenheit ist, für die  noch gilt. Da  sehr klein im Vergleich zu  ist und  sehr klein gegenüber , gilt für das Weltalter  (die gegenwärtige Epoche)

(Kosmologie)

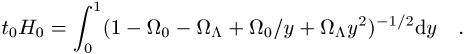
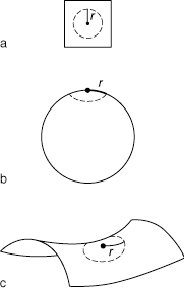
kosmologische Modelle: Die drei unterschiedlichen Raumtypen, jeweils mit Kreisen vom Radius r: a) Flacher Raum (Ebene), Krümmungsparameter k = 0; b) sphärisch gekrümmter Raum (Kugeloberfläche), k = +1; c) hyperbolisch gekrümmter Raum (Sattelfläche), k = -1.