Techniklexikon

Wirkung

Klassische Mechanik, physikalische Grösse der Dimension Energie mal Zeit. Für konservative physikalische Systeme kann die Wirkung als sog. Hamiltonsche Wirkungsfunktion, auch Wirkungsintegral oder Hamiltonsche Prinzipalfunktion genannt, definiert werden. Die Wirkungsfunktion ist das Integral S aller Wirkungen längs einer möglichen oder der tatsächlichen Bahnkurve eines Systems während einer bestimmten Zeitdauer:

 

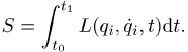
Dabei wird die Lagrange-Funktion als Funktion der verallgemeinerten Koordinaten q_i und Geschwindigkeiten  bei festgehaltenem Anfangs- und Endzustand zur Zeit t₀ und t₁ zwischen diesen Zeiten integriert. Hält man nur Anfangspunkt und -zeit fest, ist S eine Funktion des Endpunktes der Bahn bzw. der Endzeit. Die Wirkung längs der tatsächlichen Bahnkurve eines Systems ist gegenüber möglichen Vergleichsbahnen ein Extremum, im allgemeinen ein Minimum (Hamiltonsches Prinzip, Prinzip der kleinsten Wirkung). Dies wird gelegentlich so interpretiert, dass die Natur alle Bewegungen mit einem Minimum an Wirkung realisiert, womit gemeint ist, dass ein angestrebtes Ziel mit dem geringsten Aufwand an Mitteln, d.h. mit grösstem Effekt bzw. auf schnellstem Weg, erreicht wird.

Als verkürzte Wirkung oder Hamiltonsche charakteristische Funktion bezeichnet man

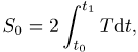
wobei T die kinetische Energie des Systems ist.

Die Dimension einer Wirkung haben auch die Produkte aus zueinander kanonisch konjugierten Variablen, z.B. das Produkt x × p_x aus Ort x und Impuls p_x jeweils bezüglich einer vorgegebenen Richtung, hier der x-Richtung.

Streng von diesem Begriff der Wirkung ist derjenige zu trennen, der beim Gesetz von Wirkung und Gegenwirkung (3. Newtonsches Axiom) im Sinne einer Wechselwirkung aller physikalischen Erscheinungen, d.h. ihrer gegenseitigen Bedingtheit, benutzt und in der Mechanik als Kraft eingeführt wird.