Techniklexikon

Matrix

Allg. Bezeichnung für die Grundmasse eines Materials, in die andere Materialien eingelagert werden können und die dann als Hüllmaterial dient. Mathematische Methoden und Computereinsatz, ein rechteckiges Schema  von Zahlen  eines Körpers K mit m Zeilen und n Spalten, für das bestimmte Rechenregeln zur Addition, Multiplikation und Inversion oder Transposition definiert sind:

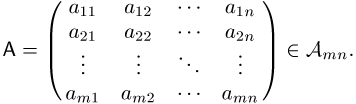
Durch Vertauschung von Spalten und Zeilen erhält man die transponierte Matrix . Wichtige Spezialfälle von Matrizen sind quadratische Matrizen mit , diagonale Matrizen mit , die Einheitsmatrix , Spalten- und Zeilenvektoren mit  bzw.  und in der numerischen Mathematik obere und untere Dreiecksmatrizen sowie Bandmatrizen, in denen nur bestimmte Nebendiagonalen besetzt sind. Jeder quadratischen Matrix kann eine skalare Grösse, die Determinante , zugeordnet werden, mit deren Hilfe sich bestimmen lässt, ob die Matrix regulär, d.h. invertierbar ist. Das Konzept der Matrix spielt eine wichtige Rolle in der linearen Algebra, da es zwischen linearen Abbildungen und Matrizen eine ein-eindeutige Beziehung gibt. Darüber hinaus sind Matrizen wegen ihrer kompakten Form sehr nützlich bei der Formulierung und Lösung linearer Gleichungssysteme oder linearer Ausgleichsprobleme. Die Addition von Matrizen ist definiert durch

Die Menge  aller Matrizen mit m Zeilen und n Spalten bildet bezüglich der Addition als Verknüpfung eine kommutative Gruppe. Die Multiplikation zweier Matrizen ist nur möglich, wenn  und ; in diesem Fall folgt sie der Rechenregel

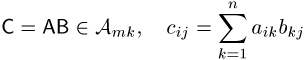
Die Matrixmultiplikation ist assoziativ, d.h. . Sie ist aber nur dann kommutativ, d.h. , wenn  und  diagonal sind und von gleicher Zeilen- und Spaltenzahl.Quadratische Matrizen, die regulär sind, d.h. , bilden bezüglich der Multiplikation als Verknüpfung eine Gruppe. Aus der Bedingung  kann die inverse Matrix prinzipiell bestimmt werden. Wegen der Nicht-Kommutativität der Matrixmultiplikation ist zu beachten: . Ausserdem gilt: .