Techniklexikon

Vektorraum

Mathematische Methoden und Computereinsatz, linearer Raum, ein Raum  über einem skalaren Körper , auch -Vektorraum genannt, der durch die Verknüpfungen  (Vektoraddition)  und  (Multiplikation mit Skalaren)  definiert ist, wobei diese Verknüpfungen den folgenden Vektorraumaxiomen genügen müssen:

(V1):  ist bezüglich der Addition eine abelsche Gruppe mit dem Nullvektor als neutralem Element;

(V2):

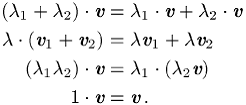
Im Falle  und  und den aus -Tupeln  gebildeten Vektoren  ist die Addition als komponentenweise Addition definiert, d.h.

und die skalare Multiplikation ist durch die Vorschrift

gegeben. Ein weiteres, recht allgemeines Beispiel eines Vektorraums ist die Menge  aller Abbildungen  einer Menge  in einen Körper  mit der punktweisen Addition und skalaren Multiplikation, d.h.  und . Konkrete Beispiele für Funktionenvektorräume sind die Menge aller stetigen oder -fach differenzierbaren, reellwertigen Funktionen, die Menge aller Funktionen, die einem bestimmten Integrierbarkeitskriterium genügen, oder die Menge aller komplexwertigen holomorphen Funktionen.

Der Betrag oder die Länge eines Vektors kann mit Hilfe der Norm gemessen werden. Häufig sind Vektorräume mit weiteren Strukturen versehen; durch die Existenz der Norm wird ein Vektroraum zu einem normierten Vektorraum. Ist in einem reellen (komplexen) Vektorraum  ein Skalarprodukt definiert, so nennt man  auch euklidischen (unitären) Vektorraum.

Jeder Vektorraum besitzt eine Basis  , d.h. eine Menge linear unabhängiger Vektoren , deren  (die Menge aller Linearkombinationen der Vektoren in ) den Vektorraum aufspannen bzw. erzeugen; bezüglich einer gegebenen Basis besitzt ein beliebiger Vektor  die Darstellung . Ein Mass für die Grösse eines Vektorraums  ist durch seine Dimension  gegeben. Besitzt  eine Basis endlich vieler Vektoren, so ist  durch die Anzahl der Basisvektoren gegeben; andernfalls setzt man  und spricht von einem unendlich dimensionalen Vektorraum. Beispiele: 1) Der Vektorraum  besitzt z.B. die  Basisvektoren  mit , wobei an der -ten Stelle des Vektors eine 1 steht; es ist , und die Basisvektoren  sind paarweise orthogonal zueinander. 2) Der Vektorraum  aller reellwertigen Polynome besitzt eine Basis, die aus allen Monomen ,  besteht; hier gilt .

Ähnlich wie sich bei Gruppen Untergruppen bilden lassen, können bei Vektorräumen Untervektorräume konstruiert werden, die gegenüber der Addition und der skalaren Multiplikation abgeschlossen sind und den Nullvektor enthalten. Als Beispiel sei der Vektorraum aller differenzierbaren Funktionen genannt; ein Untervektorraum ist dann z.B. die Menge aller Lösungen einer gegebenen homogenen gewöhnlichen linearen Differentialgleichung.

Die Vereinigung  zweier Untervektorräume  und  eines Vektorraums  ist in der Regel kein Untervektorraum. Nützlich ist jedoch das Konzept der Summe . Sind  und  Untervektorräume eines endlich-dimensionalen Vektorraums , so gilt . Gilt dabei , so nennt man  auch direkte Summe der Untervektorräume  und . Zu jedem  existiert in diesem Fall die eindeutige Zerlegung  mit  und . Ein Spezialfall direkter Summen ist die Zerlegung eines Vektorraums  in eine direkte Summe paarweise orthogonaler Unterräume , wobei für alle Vektoren  und  gilt:  und damit auch .

Der Vektorraum aller linearen Abbildungen  eines Vektorraums  in den Körper  heisst der zu  duale Vektorraum, oder kurz Dualraum, und wird mit  bezeichnet; die linearen Abbildungen werden in diesem Zusammenhang meist Linearform oder lineares Funktional genannt. In jedem endlich-dimensionalen Vektorraum  über  gilt , und es gibt zu jedem Vektor ,  eine Linearform . Diese kann mit Hilfe des Skalarproduktes gemäss  konstruiert werden. Die Vektoren  werden daher auch duale Vektoren genannt. Die Menge der Abbildungen, die den Linearformen einen Skalar zuordnen, bildet den Bidualraum , und auch hier gilt .