Techniklexikon

Diracsche Theorie des Elektrons

Quantenmechanik, Beschreibung der Bewegung relativistischer geladener Fermionen in einem elektromagnetischen Feld auf der Basis der Dirac-Gleichung. Die freie Dirac-Gleichung, die die freie Bewegung von Elektronen und Positronen beschreibt, kann zu diesem Zweck durch die sog. minimale Kopplung leicht erweitert werden. Dabei wird der Impulsoperator p_m gemäss  ersetzt (A_m: Viererpotential des elektromagnetischen Feldes); dies entspricht der Ersetzung der normalen Ableitung _m durch die kovariante Ableitung . Damit lautet die Dirac-Gleichung mit äusserer Quelle

Führt man nun durch , wobei die Matrix C durch  mit  und  definiert ist (der Index T bedeutet den transponierten Spinor bzw. die transponierte Matrix), den ladungskonjugierten Spinor y^C ein, so genügt dieser der Gleichung

und beschreibt daher Teilchen der Masse m und der Ladung  - e. Der elektrische Strom j_m kann nun in einfacher Weise relativistisch kovariant

geschrieben werden.

Mit diesem Ansatz kann die Bewegung von Elektronen in einem äusseren Potential, z.B. im Wasserstoffatom, unter Berücksichtigung relativistischer und vom Spin hervorgerufener Effekte beschrieben werden (Feinstruktur); im nichtrelativistischen Grenzfall  geht die Dirac-Gleichung mit elektromagnetischem Wechselwirkungsterm in die Pauli-Gleichung über: Führt man gemäss

,,

die Zweierspinoren c und h ein und benutzt die Diracsche Darstellung der g-Matrizen, so folgt die Dirac-Gleichung in der Form

,

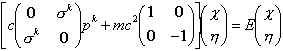d.h. als System von zwei gekoppelten Differentialgleichungen für c und h.

Für kleine Energien ist ,  und . Es ist daher wegen v/c << 1 auch h << c, für c ergibt sich . Bei Anwesenheit eines äusseren Feldes ist  zu setzen, und es folgt mit  die Pauli-Gleichung

wobei H das äussere Magnetfeld,  das (innere) magnetische Moment des Elektrons ist, das erst in der Quantenelektrodynamik durch Korrekturterme höherer Ordnung ergänzt wird (anomales magnetisches Moment). Aus höheren relativistischen Korrekturen ergibt sich u.a. die Spin-Bahn-Wechselwirkung

Der grösste Erfolg der Theorie ist jedoch die Berechnung relativistischer Korrekturen beim Spektrum des Wasserstoffatoms:

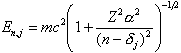
mit

Im Wasserstoffatom (Z = 1) bedeutet dies eine Aufspaltung der nichtrelativistisch noch entarteten Energieniveaus (Feinstruktur), z.B. E(2P_3/2) - E(2P_1/2) = 4,53 × 10 ^{- 4} eV. Eine Katastrophe passiert jedoch ab Z = 137: d_1/2 wird imaginär. Diese mathematische Besonderheit hängt damit zusammen, dass in starken Feldern Elektron-Positron-Paare erzeugt werden. [TB2]