Techniklexikon

anomales magnetisches Moment

des Elektrons (oder allgemein eines Fermions), die Abweichung des gyromagnetischen Verhältnisses g von der Vorhersage der Dirac-Gleichung g = 2:

a º (g - 2)/2.

Die anomalen magnetischen Momente des Elektrons und des Myons gehören zu den am genauesten bekannten Grössen in der Natur. Der Vergleich zwischen theoretischer Vorhersage und immer genaueren Messungen stimulierte ab Ende der vierziger Jahre die Entwicklung der Quantenelektrodynamik und der Renormierungstheorie. Zunehmend werden in den neuesten Präzisionsmessungen neben der QED auch Effekte aus der Theorie der Hadronen sowie des elektroschwachen Sektors des Standardmodells getestet. Die gegenwärtig genauesten experimentellen Werte für die anomalen magnetischen Momente des Elektrons bzw. Myons a_e,m sind

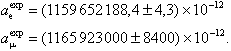
(Nobelpreise 1955 an P. Kusch und 1989 an H. Dehmelt für die Experimente zum anomalen magnetischen Moment des Elektrons). Dem stehen die theoretischen Vorhersagen von

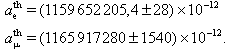
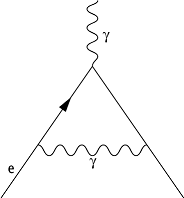
gegenüber. Der führende Beitrag  zum anomalen magnetischen Moment (Abb. 1), der für alle geladenen Leptonen identisch ist, wurde erstmals 1948 von J. Schwinger berechnet (Nobelpreis 1965):

.

a = 1/137,036 steht hier für die Feinstrukturkonstante. Unter Ausnutzung dieser Beziehung liefert die Präzisionsmessung von a_e den heute genauesten experimentellen Wert der Feinstrukturkonstanten a und hat dadurch grosse Bedeutung für die Metrologie erlangt.

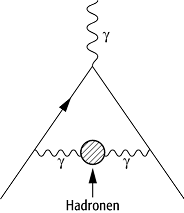
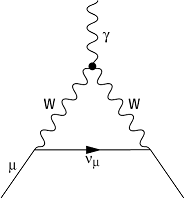
Allgemein lässt sich das anomale magnetische Moment des Elektrons als Reihenentwicklung in Potenzen von a schreiben, die durch numerisch kleine zusätzliche Terme , die z.B. von hadronischen (Abb. 2) oder elektroschwachen Effekten (Abb. 3) herrühren, ergänzt wird:

Der Koeffizient c₁ hat den Wert 1/2, auch c₂ und c₃ sind analytisch, und c₄ ist numerisch bekannt. Die Berechnung dieser Terme ist sehr kompliziert und gehört zu den grossen Leistungen der Störungstheorie. [BK1]

anomales magnetisches Moment 1: Schwinger-Diagramm, der führende Beitrag zum anomalen magnetischen Moment des Elektrons.

anomales magnetisches Moment 2: Hadronischer Beitrag zum anomalen magnetischen Moment.

anomales magnetisches Moment 3: Elektroschwacher Beitrag zum anomalen magnetischen Moment.