Techniklexikon

Phasenübergänge und kritische Phänomene

Festkörperphysik

bottom:.0001pt\'>Die grosse Vielfalt von Erscheinungen und Formen, die wir in unserer Umwelt beobachten, sowie ihr ständiger Wandel scheinen in merkwürdiger Weise mit den abstrakten Prinzipien der Physik zu kontrastieren, in denen vor allem die Unveränderlichkeit bestimmter Grössen wie Energie, Masse oder Impuls betont werden. Doch die physikalischen Gesetze stellen lediglich Rahmenbedingungen dar, innerhalb derer die Materie ihren Zustand und damit ihre Eigenschaften sehr stark wandeln kann. Für die Vielfalt der Natur sind zum einen offene Systeme verantwortlich (wie sie z.B. für die Biologie charakteristisch sind), die durch ständige Energiezufuhr und Entropieerzeugung einen thermodynamischen Nichtgleichgewichtszustand aufrechterhalten und dabei sehr komplexe Muster erzeugen können. Zum anderen spielen Umwandlungen zwischen verschiedenen (Aggregat-) Zuständen der Materie eine grosse Rolle, die dem thermodynamischen Gleichgewicht folgen. Über derartige Umwandlungen oder Phasenübergänge soll im folgenden ein Überblick gegeben werden.

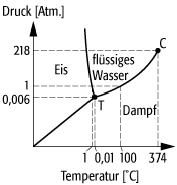
bottom:.0001pt\'>Im Gegensatz zu vielen anderen physikalischen Phänomenen stellen Phasenumwandlungen einen Teil unserer Alltagserfahrung dar. Dies gilt vor allem für Wasser und spiegelt sich beispielsweise in der Definition der Celsius-Temperaturskala (Celsius-Skala) wider, die dem schmelzenden Eis 0 °C und dem siedenden Wasser 100 °C zuordnet. Doch dies ist nur beim Standard-Atmosphärendruck von 1013,25 hPa richtig (der wiederum nur dadurch ausgezeichnet ist, dass er die Umwelt des Menschen charakterisiert). Einen Überblick über die Zustände von Wasser in einem weitem Druck- und Temperaturbereich gibt das in [7]Abb. 1 dargestellte sog. Phasendiagramm. Die feste, flüssige und gasförmige Phase sind durch Grenzlinien voneinander getrennt; beim Überschreiten einer solchen Linie (z.B. durch Temperaturerhöhung) findet ein Phasenübergang statt. Ein solches Phasendiagramm setzt thermodynamisches Gleichgewicht voraus, d.h. es enthält nur Information über den Endzustand bei vorgegebenem Druck und Temperatur - wie lange es dauert, bis das System diesen Zustand erreicht, ist eine Frage der Kinetik und geht aus dem Phasendiagramm nicht hervor.

Von besonderer Bedeutung sind die Grenzlinien zwischen den einzelnen Phasen, da sie gleichzeitig auch Koexistenzlinien (Koexistenzkurven) sind. Stellt man Druck p und Temperatur T so ein, dass sie auf einer solchen Linie liegen, so können die benachbarten Phasen gleichzeitig im Gleichgewicht existieren. Alle drei Koexistenzlinien schneiden sich im wichtigen Tripelpunkt, an dem folglich die feste, flüssige und gasförmige Phase gleichzeitig im Gleichgewicht vorliegen. Es ist daher nicht überraschend, dass dieser Punkt besonders ausgezeichnet ist und eine wichtige, materialspezifische Kenngrösse darstellt. Der Tripelpunkt von Wasser liegt bei T_T = 273,16 K und p_T = 610,5 Pa. Ebenfalls ausgezeichnet ist der Endpunkt der Koexistenzlinie von Flüssigkeit und Dampf, der für Wasser bei T_C = 647,4 K und p_C = 22,1 MPa liegt. Dieser Punkt heisst auch »kritischer Punkt«; in seiner Nähe treten die berühmten »kritischen Phänomene« auf. Obwohl der Bereich um den kritischen Punkt nur einen kleinen Teil des Phasendiagramms ausmacht, hat er die Physik in diesem Jahrhundert stark beschäftigt, da dort (weitgehend) universelles Verhalten auftritt, das unabhängig vom jeweiligen Material ist.

 

Thermodynamische Phasen und ihre Zustandsdiagramme

In der thermodynamischen Betrachtung eines Vielteilchensystems sieht man von der mikroskopischen Struktur der Systeme völlig ab und arbeitet nur mit phänomenologischen Grössen. Eine thermodynamische Phase wird daher definiert als eine makroskopische Stoffmenge mit homogenem Aufbau, die sich im Gleichgewicht mit ihrer Umgebung befindet. Falls mehrere Phasen koexistieren, sind sie durch eindeutige Grenzflächen voneinander getrennt, an denen sich makroskopische Grössen wie Dichte, Kompressibilität, Brechungszahl etc. sprunghaft ändern.

Jede Phase kann formal als ein eigenes System aufgefasst werden, dessen Energie sich durch ein zugehöriges thermodynamisches Potential beschreiben lässt und für das jeweils eine eigene Zustandsgleichung gilt (d.h. eine Verknüpfungsfunktion der relevanten Zustandsgrössen wie Druck, Temperatur, Volumen etc.). Verschiedene Phasen müssen nicht notwendigerweise mit verschiedenen Aggregatzuständen verbunden sein: Besitzt ein Material mehrere feste Modifikationen mit unterschiedlicher Kristallstruktur, so stellen diese verschiedene thermodynamische Phasen dar. Häufig werden verschiedene feste Phasen bei hohen Drücken beobachtet; dies ist z.B. bei Eis der Fall, das bei Drücken oberhalb von 200 MPa etliche Hochdruckphasen ausbildet. Von Helium sind auch zwei flüssige Phasen bekannt: Helium-I (He-I), das sich wie eine gewöhnliche viskose Flüssigkeit verhält, und unterhalb von 2,2 K das superfluide Helium-II (He-II).

Koexistierende Phasen befinden sich nur im Gleichgewicht, wenn gewisse thermodynamische Beziehungen erfüllt sind. Können z.B. zwei Phasen A und B untereinander Energie austauschen, so muss im Gleichgewicht die Temperatur der beiden Phasen gleich sein:

Bei Volumenaustausch (d.h. eine Phase kann sich auf Kosten der anderen ausdehnen) muss entsprechend der Druck identisch sein:

Ist die Anzahl der Teilchen in jeder Phase nicht konstant, weil Moleküle ausgetauscht werden, so muss im Gleichgewicht das chemische Potential für jede Molekülsorte i in beiden Phasen übereinstimmen:

Falls mehr als zwei Phasen vorliegen, gelten diese Gleichungen für jedes beliebige Paar von ihnen. Durch Abzählen solcher Gleichungen und Vergleich mit der Anzahl der thermodynamischen Variablen konnte J.W. Gibbs 1878 ganz allgemein bestimmen, wie viele Phasen maximal im Gleichgewicht koexistieren können. Die »Gibbssche Phasenregel«

begrenzt daher die Komplexität beliebiger Phasendiagramme erheblich. P steht hier für die Anzahl der koexistierenden Phasen und F für die Anzahl der thermodynamischen Freiheitsgrade (d. h. die Anzahl der Zustandsvariablen, welche unabhängig voneinander variiert werden können, ohne dass eine Phase verschwindet oder hinzukommt). K ist die Anzahl der Komponenten (unabhängigen Substanzen), aus denen das System aufgebaut ist.

Bei einkomponentigen Systemen wie z.B. Wasser kann es nur Zwei- und Dreiphasengleichgewichte geben. Im Einphasenbereich, z.B. Wasserdampf, ist P = 1, so dass dort F = 2 Freiheitsgrade vorliegen. Daher ist das Einphasengebiet im p-T-Diagramm eine Fläche, und sowohl Temperatur als auch Druck können unabhängig verändert werden, ohne dass ein Phasenübergang stattfindet. Falls zwei Phasen koexistieren, ergibt sich nur noch ein Freiheitsgrad und damit eine Koexistenzlinie. Für die Koexistenz aller drei Phasen ergibt sich F = 0, d.h. keine Zustandsvariable ist mehr frei wählbar, und das System ist nur an einem ausgezeichneten Punkt - dem Tripelpunkt - thermodynamisch stabil.

Die Phasendiagramme einkomponentiger Stoffe werden typischerweise in Abhängigkeit vom Gleichgewichtsdruck p und der Temperatur T dargestellt. Die Linien der Zweiphasen-Koexistenz heissen Dampfdruckkurve (gasförmig-flüssig), Sublimations(druck)kurve (gasförmig-fest) und Schmelz(druck)kurve (flüssig-fest). Bei binären Mischungen wird wegen P = 2 die Zusammensetzung als weiterer Freiheitsgrad zur vollständigen Beschreibung benötigt. Mehrkomponentige Systeme zeigen eine reiche Vielfalt von Zustandsdiagrammen auf Grund des stark temperatur- und zusammensetzungsabhängigen Mischungsverhaltens der Komponenten.

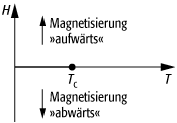
Die thermodynamische Behandlung von Phasenübergängen erlaubt es, Umwandlungen in äusserlich sehr unterschiedlichen Systemen auf eine einheitliche Grundlage zu stellen und Parallelen aufzuzeigen. Beispielsweise kann bei Supraleitern der Übergang vom normalleitenden Zustand in den supraleitenden Zustand als Phasenübergang aufgefasst werden, wobei auf den Achsen des zugehörigen Phasendiagramms das äussere Magnetfeld H und die Temperatur aufgetragen sind. Ein weiteres, wichtiges Beispiel sind magnetische Phasenübergänge, da das Auftreten einer spontanen Magnetisierung unterhalb einer gewissen Ordnungstemperatur nicht nur experimentell gut zugänglich ist, sondern auch theoretische Beschreibungen wie das Ising-Modell oder Heisenberg-Modell inspiriert hat, die heute von paradigmatischer Bedeutung für die Physik der Phasenübergänge sind. Das Phasendiagramm des Ising-Modells ist in [8]Abb. 2 gezeigt; es gilt allgemein für einen Ferromagneten (ferromagnetische Substanzen), dessen Magnetisierung ausschliesslich parallel zu einer ausgezeichneten (»leichten«) Kristallachse erfolgen kann. In diesem Fall gibt es nur zwei ferromagnetische Phasen, deren Magnetisierungen entweder parallel oder antiparallel zu dieser Achse verlaufen. Wenn ein äusseres Magnetfeld H anliegt, existiert je nach Richtung von H nur eine der beiden Phasen. Falls H = 0 ist, koexistieren beide Magnetisierungen in Form von Domänen. Die horizontale Koexistenzlinie in [9]Abb. 2 stellt daher das Analogon zur Dampfdruckkurve in [10]Abb. 1 dar, wobei das äussere Magnetfeld H dem Druck p entspricht. Beide Kurven enden in einem kritischen Punkt. In [11]Abb. 1 existiert bei Temperaturen oberhalb der kritischen Temperatur T_C nur noch eine einzige, fluide Phase, da Flüssigkeit und Dampf ununterscheidbar geworden sind; dem entspricht in [12]Abb. 2 der paramagnetische Kristallzustand.

bottom:.0001pt\'> 

bottom:.0001pt\'>Diskontinuierliche und kontinuierliche Umwandlungen

bottom:.0001pt\'>Verschiedene Phasen einer Substanz lassen sich durch Veränderung äusserer Parameter ineinander umwandeln, wenn dabei im Phasendiagramm die Koexistenzkurve gekreuzt wird. Der zugehörige Phasenübergang ist - ausser am kritischen Punkt - diskontinuierlich. Diese Bezeichnung spiegelt die mit der Umwandlung einhergehende, sprunghafte Veränderung thermodynamischer Zustandsfunktionen wider. Beispielsweise ändert sich beim Verdampfen von Wasser sprunghaft die Dichte, wenn Flüssigkeit in Dampf umgewandelt wird. Auch die Entropie ändert sich unstetig, da während der Zweiphasen-Koexistenz bei konstanter Temperatur T ständig Wärme zugeführt werden muss, um die Flüssigkeit nach und nach in Dampf zu überführen. Der Entropiesprung DS ist also direkt mit der Umwandlungswärme L = TDS (»latente Wärme«) verbunden. Beide Diskontinuitäten hängen über die Clausius-Clapeyron-Gleichung mit der Steigung der Koexistenzlinie zusammen:

bottom:.0001pt\'>

bottom:.0001pt\'>wobei S, L und das Volumen V sich jeweils auf ein Mol der Phasen A und B beziehen.

bottom:.0001pt\'>Die Clausius-Clapeyron-Gleichung gilt auch für die Schmelz- und Sublimationskurve. Da das Verdampfen, Schmelzen und Sublimieren Umwandlungen in einen weniger geordneten Zustand darstellen, sind die zugehörigen latenten Wärmen stets positiv. Die Übergänge fest  gasförmig und flüssig  gasförmig sind mit positiven Volumenänderungen verbunden, so dass die Sublimations- und Dampfdruckkurven immer eine positive Steigung besitzen. Die molaren Volumina eines Festkörpers und einer Flüssigkeit sind jedoch vergleichbar, so dass das Vorzeichen der Volumenänderung beim Schmelzen auch negativ sein kann. Wasser ist einer der wenigen Fälle, in denen die Flüssigkeit dichter als der Festkörper ist, daher weist die Schmelzkurve in [13]Abb. 1 eine negative Steigung auf.

bottom:.0001pt\'>Bei diskontinuierlichen Phasenübergängen sind Überhitzung und Unterkühlung möglich, wenn die Keimbildung erschwert ist. Grenzflächeneffekte spielen dabei auf Grund der Koexistenz zweier unterschiedlicher Phasen eine wichtige Rolle.

bottom:.0001pt\'>Ganz anders liegen die Verhältnisse bei einem Phasenübergang am kritischen Punkt: dort unterscheiden sich die Phasen nur noch infinitesimal wenig, so dass ihre physikalischen Eigenschaften identisch sind. Umwandlungen am kritischen Punkt werden daher kontinuierlich genannt. Eine unmittelbare Konsequenz ist, dass mit ihnen kein Entropiesprung verbunden ist und somit keine latente Wärme auftritt. In der Nähe des kritischen Punktes können Keime der einen Phase sich in der jeweils anderen Phase praktisch ohne energetischen Aufwand ausbreiten, da die aufzubringende Grenzflächenenergie (Grenzflächenspannung) oder Ausdehnungsarbeit zu vernachlässigen ist. Am Umwandlungspunkt erfolgt die gesamte Umwandlung schlagartig - weder Überhitzung noch Unterkühlung sind möglich.

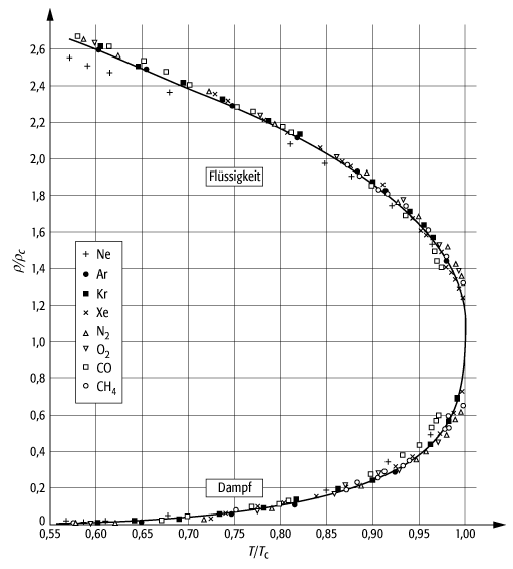
bottom:.0001pt\'>Die Kontinuität der Zustände am kritischen Punkt wird in [14]Abb. 3 für verschiedene einkomponentige Substanzen beispielhaft gezeigt. Bei Temperaturen unterhalb der kritischen Temperatur T_C koexistieren Flüssigkeit und Dampf mit verschiedenen Dichten. An der wohldefinierten Grenzfläche zwischen beiden Phasen tritt ein Dichtesprung auf, der entlang der Dampfdruckkurve immer kleiner wird und am kritischen Endpunkt ganz verschwindet. Da es jenseits des kritischen Punktes keinen Unterschied mehr zwischen der flüssigen und der gasförmigen Phase gibt, ist es daher durch eine entsprechende Prozessführung möglich, eine Flüssigkeit reversibel zu verdampfen, ohne eine Koexistenzlinie zu kreuzen. Andererseits ist es nur für Temperaturen unterhalb des kritischen Punktes möglich, ohne Kühlen allein durch Erhöhung des Drucks die Dampfphase zu verflüssigen. Dies ist von grosser praktischer Bedeutung, da Substanzen mit niedrigen kritischen Temperaturen (z.B. He mit T_C = 5,2 K) somit schwer verflüssigbar sind.

bottom:.0001pt\'>Bei Annäherung an den kritischen Punkt kann bei ansonsten durchsichtigen Substanzen das interessante Phänomen der kritischen Opaleszenz (kritischen Lichtstreuung) beobachtet werden. Dabei erzeugen thermische Fluktuationen überall unbeständige flüssigkeits- und dampfartige Bereiche, die gross genug sind, um Licht zu streuen. Die Substanz erscheint dann milchig und trüb. Am kritischen Punkt sind diese Fluktuationen so stark angewachsen, dass die Grenzfläche zwischen Flüssigkeit und Dampf verschwindet.

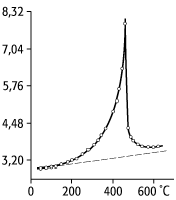
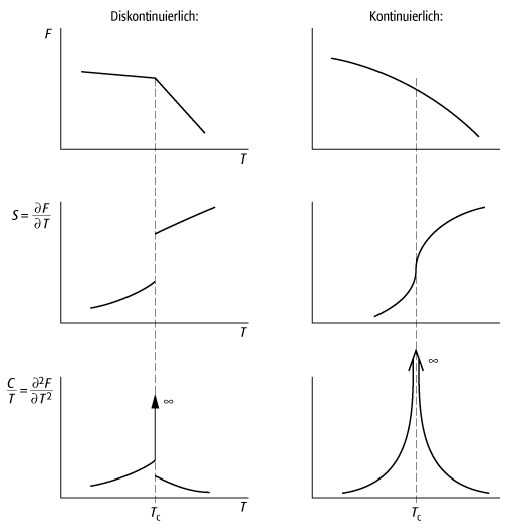
bottom:.0001pt\'>Ein früher Versuch der systematischen Klassifikation von Phasenübergängen wurde 1925 von P. Ehrenfest unternommen, der ein Ordnungsschema vorschlug, in dem zwischen Phasenübergängen erster, zweiter, dritter etc. Ordnung unterschieden wurde. Dieses Schema ist heute überholt; es soll hier jedoch trotzdem erwähnt werden, weil es den Sprachgebrauch bei Phasenumwandlungen nachhaltig geprägt hat. Die Ehrenfestsche Klassifikation stellt eine Verallgemeinerung der Eigenschaften diskontinuierlicher Phasenübergänge dar, die dort Phasenübergänge erster Ordnung heissen. Die Bezeichnungsweise rührt daher, dass bei diesen Umwandlungen die freie Energie zwar stetig verläuft, jedoch am Umwandlungspunkt einen Knick aufweist, so dass die ersten Ableitungen der freien Energie unstetig sind. Die latente Wärme ergibt sich dann beispielsweise aus dem Sprung in der Entropie etc. Um auch Umwandlungen ohne latente Wärme beschreiben zu können, wurde deshalb ein Phasenübergang n-ter Ordnung so definiert, dass im Umwandlungspunkt die freie Energie und ihre Ableitungen bis zur (n - 1)-ten Ordnung stetig sind, während die n-te Ableitung unstetig ist. Bei Phasenübergängen zweiter Ordnung würde man also erwarten, dass die Entropie sich stetig verhält, während die spezifische Wärme einen endlichen Sprung aufweist. Es hat sich jedoch experimentell herausgestellt, dass bei kontinuierlichen Umwandlungen die spezifische Wärme um so grösser wird, je näher man an den kritischen Punkt kommt ([15]Abb. 4 zeigt ein typisches Beispiel). Derartige Singularitäten sind charakteristisch für kontinuierliche Umwandlungen. Man beachte, dass die spezifische Wärme schon weit vor dem eigentlichen Phasenübergang anzusteigen beginnt. Auf Grund der Kurvenform, die an den griechischen Buchstaben l erinnert, heissen solche Phasenumwandlungen in der älteren Literatur auch l-Übergänge. Da Phasenübergänge dritter und höherer Ordnung nie beobachtet wurden, unterscheidet man heute nur noch zwischen diskontinuierlichen und kontinuierlichen Phasenumwandlungen. Die Ausdrucksweise »Phasenübergang von erster (bzw. zweiter) Ordnung« ist jedoch fest eingebürgert und wird mittlerweile synonym für diskontinuierliche (bzw. kontinuierliche) Umwandlungen benutzt. Ihre Charakteristika sind in [16]Abb. 5 gegenübergestellt.

bottom:.0001pt\'> 

bottom:.0001pt\'>Kritische Phänomene

bottom:.0001pt\'>Phasenübergänge am kritischen Punkt können auch unter dem Aspekt betrachtet werden, dass sich unterhalb der kritischen Temperatur T_C spontan eine gewisse makroskopische Ordnung ausbildet. Diese Ordnung wird dann durch einen Ordnungsparameter beschrieben, dessen thermodynamischer Mittelwert oberhalb von T_C Null ist, unterhalb von T_C dagegen endliche Werte annimmt. Die Identifizierung des richtigen Ordnungsparameters ist nicht immer trivial; bei Ferromagneten ist es jedoch nicht überraschend, dass die Magnetisierung die Rolle des Ordnungsparameters spielt. Bei Fluiden wird die Differenz der Dichten von Flüssigkeit und Dampf zur Definition eines Ordnungsparameters herangezogen (siehe [17]Abb. 3). Bei Annäherung an den kritischen Punkt geht der Ordnungsparameter stetig gegen Null und folgt dabei einem Potenzgesetz:

bottom:.0001pt\'>

bottom:.0001pt\'>Die dimensionslose Zahl b wird auch als kritischer Exponent bezeichnet. Verschiedene Materialkonstanten divergieren am kritischen Punkt, z.B. die Suszeptibilität von Ferromagneten oder die Kompressibilität von Fluiden. Auch hier werden experimentell Potenzgesetze beobachtet:

bottom:.0001pt\'>

bottom:.0001pt\'>g ist ebenfalls ein kritischer Exponent.

bottom:.0001pt\'>Das Auftreten von Potenzgesetzen im Zusammenhang mit Phasenübergängen ist schon lange bekannt. Van der Waals gab in seiner Dissertation erstmals die nach ihm benannte Zustandsgleichung an, mit der sich die Kondensation eines Gases beschreiben lässt. Aus dieser Theorie lässt sich b = 1 / 2 und g = 1 ableiten. Dieselben Werte für b und g erhält man aus der Weiss\'schen Theorie des Ferromagnetismus. Wie Landau 1937 gezeigt hat, ist dies kein Zufall, da van der Waals wie auch Weiss von der Annahme ausgegangen sind, dass jedes Molekül bzw. jeder Elementarmagnet eine Umgebung mit gleicher mittlerer Dichte bzw. Magnetisierung »sieht«. Derartige Theorien beschreiben also ein wechselwirkendes Vielteilchensystem durch ein mittleres, effektives Feld, das auf ein beliebig herausgegriffenes Teilchen wirkt, und ignorieren lokale Fluktuationen (»mean field theory« oder »Molekularfeldtheorie«).

bottom:.0001pt\'>Experimentell findet man für Fluide statt der obigen »Molekularfeld-Exponenten« jedoch  und . Kritische Exponenten wurden an sehr vielen kontinuierlichen Phasenübergängen experimentell bestimmt. Es hat sich dabei herausgestellt, dass diese Exponenten weitgehend universellen (d. h. nicht materialspezifischen) Charakter besitzen. [18]Abb. 3 zeigt dies in eindrucksvoller Weise für acht sehr unterschiedliche Substanzen, deren kritische Temperaturen und Drücke weit auseinanderliegen. Der Begriff der Universalität bezieht sich aber nicht nur auf Phasenübergänge desselben Typs in verschiedenen Substanzen, sondern umfasst auch ganz verschiedene Formen von Phasenumwandlungen. Beispielsweise werden dieselben kritischen Exponenten für Fluide, einachsige Ferro- und Antiferromagnete sowie Ordnungs/Unordnungs-Übergänge in binären Legierungen (z.B. CuZn, siehe [19]Abb. 4) gemessen. Kritische Exponenten sind jedoch nicht völlig universell. Es hat sich herausgestellt, dass für die Werte der Exponenten zwei Parameter relevant sind: die räumliche Dimension d des betrachteten Systems und die Zahl n der Freiheitsgrade des Ordnungsparameters. Alle kontinuierlichen Phasenübergänge werden entsprechend den Werten von d und n in sog. Universalitätsklassen eingeteilt. Dies erklärt die Übereinstimmung der kritischen Exponenten für dreidimensionale Magnete mit nur zwei Einstellmöglichkeiten der Magnetisierung und Fluide - mit d = 3 und n = 1 gehören beide zur Universalitätsklasse des dreidimensionalen Ising-Modells. Man kann mathematisch zeigen, dass sich die »Molekularfeld-Exponenten« erst oberhalb von d = 4 ergeben.

Die theoretische Berechnung kritischer Exponenten zählt zu den schwierigsten Aufgaben der Physik und wurde erst mit der Entwicklung der Renormierungsgruppentheorie durch K. Wilson systematisch möglich; er erhielt für diese Leistung 1982 den Nobelpreis. Renormierungsverfahren lassen sich immer dann anwenden, wenn das betrachtete Problem die Eigenschaft der Selbstähnlichkeit besitzt (d.h. es sieht auf unterschiedlichen Skalen qualitativ gleich aus). Bei kritischen Phänomenen ist diese Skaleninvarianz am kritischen Punkt wegen der divergierenden Korrelationslänge der statistischen Fluktuationen gegeben. Bei magnetischen Systemen gibt es dann korrelierte Cluster jeder Magnetisierungsrichtung auf allen Längenskalen; bei fluiden Systemen findet man entsprechend Gasblasen und Flüssigkeitströpfchen jeder Grösse. Der kritische Punkt ist also durch eine zusätzliche Symmetrieeigenschaft - die Invarianz gegenüber Skalentransformationen - ausgezeichnet.

 

Literatur:

H.E. Stanley, Introduction to phase transitions and critical phenomena, Oxford University Press, Oxford, 1971.

C. Domb und M.S. Green (Hrsg.), Phase transitions and critical phenomena, Vol. 1-6, Academic Press, London 1972-1976.

C. Domb und J.L. Lebowitz (Hrsg.), Phase transitions and critical phenomena, Vol. 7- , Academic Press, London 1983- .

J.M. Yeomans, Statistical mechanics of phase transitions, Oxford University Press, Oxford, 1992.

 

Phasenübergänge und kritische Phänomene 1: Kritische Temperaturen und Drücke verschiedener Gase.