Techniklexikon

lineare Abbildung

eine Funktion, Operator oder Abbildung  von einem über dem Körper K definierten Vektorraum V in den ebenfalls über K definierten Vektorraum W mit der Eigenschaft, dass für alle Vektoren  und Skalar  gilt:

Lineare Abbildungen zwischen endlich dimensionalen Vektorräumen lassen sich vollständig durch Matrizen beschreiben; bei gegebener Basis, d.h. einem System aus Basisvektoren b_i, sind die Spaltenvektoren der Matrix gerade die Bildvektoren der auf die Vektoren b_i angewendeten Abbildung f. Beispiel: Die Matrixdarstellung der Abbildung , die eine Drehung um den Winkel  gegen den Uhrzeigersinn darstellt, lautet

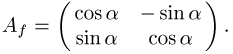
Beispiele für lineare Abbildungen auf unendlich dimensionalen Vektorräumen (hier: Funktionenräume) sind die Differentiation und Integration. Lässt sich zeigen, dass eine gegebene lineare Abbildung bestimmte Eigenschaften hat, z.B. dass sie injektiv (eindeutig umkehrbar) oder bijektiv (injektiv und surjektiv, d.h. den gesamten Zielraum erreichend) ist, so kann man daraus nützliche Schlüsse ziehen. Das Urbild des Nullvektors im Zielraum einer injektiven linearen Abbildung ist genau der Nullvektor des Ursprungsraums. Eine bijektive lineare Abbildung bildet eine Menge linear unabhängiger Vektoren wieder auf ein System unabhängiger Vektoren ab.