Techniklexikon

Störungstheorie

Quantenmechanik,

1) Mechanik: Störungsrechnung.

2) Quantenmechanik: häufig benutzte Methode zur näherungsweisen Berechnung von Eigenfunktionen und Eigenwerten des Hamilton-Operators und damit zur genäherten Bestimmung der Bewegung quantenphysikalischer Systeme. Die Störungstheorie ist anwendbar, wenn die Lösung für das freie, ungestörte System mit dem Hamilton-Operator  bereits bekannt ist und der Hamilton-Operator des wechselwirkenden, gestörten Systems die Form  hat, wobei  ein kleiner Parameter, der Störparameter, und  der Hamilton-Operator der Störung ist. Je nachdem, ob man Lösungen der zeitabhängigen oder der zeitunabhängigen (stationären) Schrödinger-Gleichung konstruiert, spricht man von der zeitabhängigen oder Diracschen bzw. der zeitunabhängigen oder Schrödingerschen Störungstheorie; die Bornsche Näherung ist ebenfalls eine Störungstheorie speziell für Streuprobleme.

1) Die Schrödingersche zeitunabhängige Störungstheorie gestattet nur die Behandlung stationärer Probleme. Man macht für die Eigenfunktionen  bzw. die Eigenwerte  von  einen Potenzreihenansatz

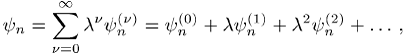
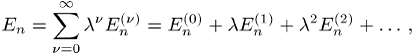
wobei  bzw.  Eigenfunktion bzw. Eigenwert von  ist, d.h. . Das Eigenwertproblem für  wird dann sukzessive gelöst, indem man nur Potenzen erster, zweiter usw. Ordnung von  betrachtet und die Annahme macht, dass sich die zugehörigen Funktionen  der ersten, zweiten usw. Näherung als Linearkombinationen der Eigenfunktionen nullter Näherung, , schreiben lassen, d.h. . Liegt keine Entartung vor, so erhält man die Eigenwerte ,  usw. Liegt dagegen Entartung vor, haben also N Zustände  dieselbe Energie , dann spaltet der N-fach entartete Eigenwert  bei Störung in N verschiedene Eigenwerte  auf, wobei sich die  aus der Lösung der Säkulardeterminante  ergeben.

2) Die Diracsche zeitabhängige Störungstheorie gestattet die näherungsweise Bestimmung der Übergänge von quantenphysikalischen Systemen unter dem Einfluss einer möglicherweise zeitabhängigen Störung . Man macht hierbei den Ansatz

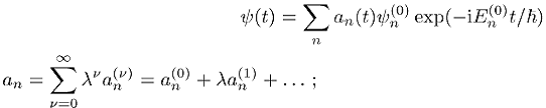
aus der zeitabhängigen Schrödinger-Gleichung ergibt sich die Bewegungsgleichung der zeitabhängigen Koeffizienten  zu , und in erster Näherung folgt

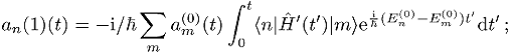
in dieser Form wurde die zeitabhängige Störungstheorie von Dirac 1926 entwickelt und auf die halbklassische Strahlungstheorie angewandt (goldene Regel).

3) Quantenfeldtheorie: Vorgehensweise zur Berechnung der vollen Green-Funktionen in einer wechselwirkenden Feldtheorie mit kleinem Kopplungsparameter l. Dazu führt man als erzeugendes Funktional für die Green-Funktionen das Pfadintegral (hier für eine skalare Feldtheorie  mit  und )

ein, das wegen  als

geschrieben werden kann (: Normierungskonstante), wobei

das erzeugende Funktional des freien Propagators

ist, welches sich ohne explizite Funktionalintegration durch partielle Integration und Fourier-Transformation in die Form

mit

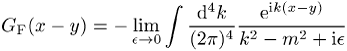
bringen lässt. Für die wechselwirkende Theorie kann das erzeugende Funktional allerdings nicht exakt berechnet werden; man entwickelt vielmehr die Exponentialfunktion in

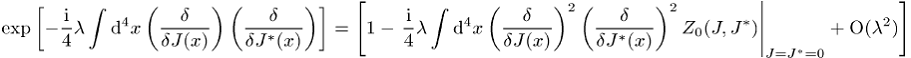
und leitet daraus den Propagator der wechselwirkenden Theorie ab,

,

an dem sich (nach Fourier-Transformation in den Impulsraum) die Feynman-Regeln

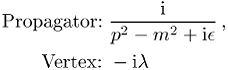
ablesen lassen. Auf diese Weise lassen sich in jeder Ordnung von  sämtliche Beiträge zur Green-Funktion in Form von Feynman-Diagrammen angeben; analog verfährt man auch – unter Berücksichtigung gewisser Besonderheiten – für fermionische Felder und schliesslich für Eichtheorien.