Techniklexikon

Instantonen

Quantenmechanik, solitonische Lösungen der vierdimensionalen euklidischen Feldtheorie. Sie können als quantenmechanisches Tunneln zwischen verschiedenen Vakuumzuständen interpretiert werden. Diese Lösungen haben die überraschende Eigenschaft, dass sie mit topologischen Methoden (Topologie) studiert und ihnen bestimmte Windungszahlen zugeordnet werden können. Instantonen haben sich als mächtiges Werkzeug zur Erforschung des nicht-störungstheoretischen Bereichs von Eichtheorien erwiesen.

In euklidischen Yang-Mills-Theorien interessiert man sich für selbst-duale klassische Lösungen , also solche mit der Eigenschaft . Man kann zeigen, dass die zugehörige Wirkung endlich und proportional zur sog. Windungszahl n ist,

.

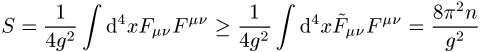Dieses Resultat zeigt deutlich den nicht-störungstheoretischen Charakter des Instantons: sein Beitrag zum Pfadintegral ist proportional zu exp(-1 / g²) und somit niemals in endlicher Ordnung der Störungstheorie zu approximieren.

Das Vektorpotential des Instantons ist im Unendlichen ein reines Eichfeld, , wobei W ein Element der Gruppe SU(2) ist (Verallgemeinerungen entsprechend), welches für jeden Punkt x_m einer dreidimensionalen Sphäre S₃ generiert werden kann; jede reine Eichkonfiguration ist also durch eine Hypersphäre S₃ gekennzeichnet. Es lässt sich zeigen, dass der Index n den Grad einer nicht-trivialen Abbildung  angibt, wobei die eine Hypersphäre der durch W gegebene Raum von SU(2) ist und die andere Hypersphäre den physikalischen Raum (den Rand des euklidischen Raumes) repräsentiert. Das bedeutet, dass das naive Vakuum der Yang-Mills-Theorie das falsche ist; vielmehr existieren unendlich viele topologisch verschiedene Vakua, wobei jedes durch eine ganze Zahl n gekennzeichnet ist.

Die Einführung von Instantonen in die Quantenchromodynamik (QCD) löst das axiale U(1)-Problem, generiert aber ein anderes, das starke CP-Problem. In der Anwesenheit von Instantonen ist der Axialvektorstrom gegeben durch

,

und das Integral

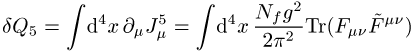
verschwindet nicht (\'t Hooft). Deshalb gibt es keine U_A(1)-Symmetrie, und man braucht keine Goldstone-Bosonen (Goldstone-Theorem) zu suchen. Andererseits ist der neue Term in der Lagrange-Dichte paritäts- und auch CP-verletzend. Experimentelle Beobachtungen schränken den Anteil dieser Wirkung auf kleiner als 10^-9 ein. Dafür aber gibt es keine Erklärung.