Techniklexikon

Distributionen

Quantenmechanik

bottom:.0001pt\'>Distributionen - verallgemeinerte Funktionen (englisch "generalized functions") - sind stetige lineare Funktionale auf geeigneten Funktionenräumen. (Für die genauen Definitionen s.u. Abschnitt "Definitionen".)

bottom:.0001pt\'>Sie stellen eine Verallgemeinerung des klassischen Funktionsbegriffs dar, bei der die übliche Zuordnung einer Funktion von Zahlen auf andere Zahlen (deren Funktionswerte), also

bottom:.0001pt\'>Funktion: Zahl   Zahl

bottom:.0001pt\'>zu einer Zuordnung

bottom:.0001pt\'>Distribution: Funktion   Zahl

bottom:.0001pt\'>erweitert wird. Die Distribution ordnet dabei der ganzen Funktion (der sogenannten "Testfunktion", siehe unten) einen Zahlwert zu.

bottom:.0001pt\'>Mit dieser abstrakten Verallgemeinerung des Funktionsbegriffs wird erreicht, dass sie eine exakte Lösung von mathematischen Problemen gestattet, welche sonst - nur mit Methoden der klassischen Analysis - nicht möglich oder formulierbar wäre. Im klassischen Funktionssinn hätten die gestellten Probleme keine Lösung. Zu solchen Situationen führen insbesondere viele physikalisch motivierte Problemstellungen, so dass sich der mathematische Aufwand, gemessen an der Relevanz für die praktische Verwertbarkeit in der Physik, durchaus lohnt. Allerdings wird häufig in physikalischen Anwendungen lediglich darauf hingewiesen, dass es sich bei den zur Lösung des gestellten Problems benötigten Objekten um Distributionen handelt, für die bestimmte Rechenregeln zu beachten sind und mit denen bestimmte Manipulationen nicht durchgeführt werden dürfen. Je nach Ziel oder persönlicher Neigung empfindet man ein solches Vorgehen als mehr oder weniger gerechtfertigt oder letztlich doch unbefriedigend.

bottom:.0001pt\'>Die wichtigsten und bekanntesten Beispiele stellen die Diracschen d-Distributionen (d-Funktion)  dar, mit deren Hilfe idealisierte Punktdichteverteilungen (daher ihr Name) behandelt werden können, wie z.B. Punktladungen, Punktdipole u.a., und welche immer noch häufig als Einstieg in die Theorie der Distributionen verwendet werden. Als Beispiel und zur Illustration der oben erwähnten Sachverhalte kann das Poisson-Gesetz für eine Einheits-Punktladung in der Elektrodynamik dienen, bei dem die dreidimensionale d-Distribution  bei der Anwendung des Laplace-Operators

bottom:.0001pt\'>auf die Funktion  im ganzen Raum auftritt:

bottom:.0001pt\'>

bottom:.0001pt\'>Daneben erscheinen diese Diracschen d-Distributionen oft als "kontinuierliche" Kronecker-Symbole, z.B. in der Quantenmechanik in der Form , oder in Vertauschungsrelationen der Form

bottom:.0001pt\'>Ein weiteres wichtiges Beispiel (und historisch vielleicht das erste) stellt die Heavisidesche Stufen- oder Sprungfunktion V dar, deren Ableitung  gerade d ist:

bottom:.0001pt\'>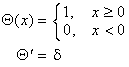

bottom:.0001pt\'>In der Theorie der Fourier-Integrale (Fourier-Analysis) lösen Distributionen das Problem, dass oftmals ganz einfache Funktionen keine Fourier-Transformierte im gewöhnlichen Funktionensinn haben, jedoch beispielsweise in der Behandlung von partiellen linearen Differentialgleichungen mit Randbedingungen alle auftretenden Funktionen als Fourier-Integral ausgedrückt werden müssen. So besitzen konstante Funktionen keine Fouriertransformierte - die Fouriertransformierte der 1 ist die Diracsche d-Distribution; dies liefert umgekehrt eine besonders für die Physik wichtige Integraldarstellung der d-Distribution, dazu siehe unten.

bottom:.0001pt\'> 

bottom:.0001pt\'>Definitionen

bottom:.0001pt\'>Für die genaue Definition benötigt man zunächst einige Begriffe. Ausgangspunkt bilden dabei besonders "gutartige" Funktionen, mit denen man die sogenannten Testfunktionenräume bildet, auf welchen die Distributionen dann als stetige lineare Funktionale definiert werden. Besonders "gut" sind beliebig oft stetig differenzierbare Funktionen , die allerdings zusätzlich auch noch besonders "gut" integrierbar sein müssen. Dazu betrachtet man den mathematischen Abschluss der Menge , welche Träger von j heisst, geschrieben supp(j) (aus dem englischen "support"). Grundlage aller folgenden Definitionen ist der lineare Raum D aller Funktionen, welche beliebig oft stetig differenzierbar sind und einen kompakten Träger besitzen (d.h. sie sind auch über beliebige Gebiete integrierbar). Die Elemente dieses Raumes heissen Testfunktionen oder Grundfunktionen. Ein Beispiel einer solchen Testfunktion ist t(x).

bottom:.0001pt\'>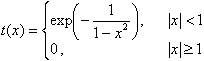

bottom:.0001pt\'>deren Träger die Kugel vom Radius 1 ist.

bottom:.0001pt\'>Die Menge der linearen Funktionale T, d.h. der linearen Abbildungen T:  in den Körper des Vektorraums, bildet selbst einen Vektorraum, den sog. algebraischen Dualraum von  D . Um den sog. topologischen Dualraum D von  D , d.h. den Raum der stetigen linearen Funktionale auf  D  zu konstruieren, benötigt man einen Konvergenzbegriff in  D . Man sagt, dass eine Folge f_n von Funktionen in  D  konvergiert, geschrieben , wenn zwei Bedingungen erfüllt sind:

bottom:.0001pt\'>1. Es gibt ein Kompaktum K, so dass  und

bottom:.0001pt\'>2. für alle Multiindizes a gilt, dass alle partiellen Ableitungen , d.h. gleichmässig konvergieren. Dann heisst ein lineares Funktional T auf D stetig, wenn aus  in D folgt, dass auch .

bottom:.0001pt\'>Solche stetigen linearen Funktionale T auf D heissen Distributionen. Man schreibt

bottom:.0001pt\'>

bottom:.0001pt\'>und  für den Raum aller Distributionen.

bottom:.0001pt\'>Von besonderer Bedeutung für die Physik sind die d_x-Distributionen, welche für alle Punkte  definiert sind durch . Die Anwendung der d_x-Distribution auf die Testfunktion liefert als Zahlenwert den Funktionswert am Punkt x (daher gibt es strenggenommen für jeden Punkt des Raumes eine d-Distribution).

bottom:.0001pt\'>Eine wichtige Möglichkeit, stetige lineare Funktionale auf D zu konstruieren, d.h. Distributionen zu erzeugen, ergibt sich durch Integration: Jede lokal integrierbare Funktion f erzeugt eine Distribution [f] durch

bottom:.0001pt\'>.

bottom:.0001pt\'>Alle Distributionen, welche sich auf diese Art durch Integration ergeben, heissen regulär, alle Distributionen, welche nicht regulär sind, heissen singulär. Dazu gehören insbesondere die d-Distributionen. Die in der Physik oft zu findende Schreibweise

bottom:.0001pt\'>

bottom:.0001pt\'>ist rein formal zu verstehen, gemeint ist

bottom:.0001pt\'>.

bottom:.0001pt\'>Obige Gleichung kann nicht durch einen Grenzübergang mit einer Funktionenfolge realisiert werden, da dies den Lebesgueschen Grenzwertsatz verletzen würde.

bottom:.0001pt\'> 

bottom:.0001pt\'>Einige Rechenregeln

bottom:.0001pt\'>Ein Vorteil obiger Definition ist, dass man nun eine lineare Substitution und beliebige partielle Ableitungen von Distributionen über die jeweilige Operation der Testfunktionen definieren kann. Die folgenden Rechenregeln, welche häufig in physikalischen Anwendungen benötigt werden, lassen sich leicht für reguläre Distributionen herleiten und werden entsprechend - per definitionem - auf singuläre Distributionen übertragen.

bottom:.0001pt\'>Ist y = Ax + b eine lineare Transformation von , wobei A eine n ´ n-Matrix und  ist, und ist g(x) = f(Ax + b) sowie [g] die von g erzeugte Distribution, so gilt

bottom:.0001pt\'>.

bottom:.0001pt\'>Genauso, wie man diese Formel für reguläre Distributionen mit Hilfe der Transformationsformel für mehrdimensionale Integrale im  zeigen kann, führt Produktintegration unter Ausnutzung der Tatsache, dass die Integranden wegen der kompakten Träger der Testfunktionen im Unendlichen verschwinden, auf die folgende Rechenvorschrift:

bottom:.0001pt\'>.

bottom:.0001pt\'>Distributionen besitzen also Ableitungen beliebiger Ordnung. Beispiel: .

bottom:.0001pt\'>Damit kann man folgende Rechenregeln zeigen:

bottom:.0001pt\'> konstant,

bottom:.0001pt\'>,

bottom:.0001pt\'>wobei x_i die einfachen Nullstellen der Funktion f sind.

bottom:.0001pt\'>Für die Gültigkeit der bisherigen Überlegungen ist von zentraler Bedeutung, dass die Testfunktionen im Unendlichen verschwinden. Man kann die Definitionen nun noch erweitern, indem man diese Voraussetzung etwas abschwächt und als Testfunktionen auch solche zulässt, die für die auftretenden Integrationen im Unendlichen hinreichend schnell "abfallen". Dies führt auf einen Funktionenraum  F , den sog. Schwartzschen Raum der schnell-fallenden Funktionen ("schneller als jede Potenz von 1/x fallend"). Die mathematisch genaue Definition lautet: Eine beliebig oft stetig differenzierbare Funktion f auf dem  heisst schnell-fallend (und ist ein Element von  F ), wenn zu jedem Multiindex a und zu jedem  eine Konstante c existiert, so dass

bottom:.0001pt\'>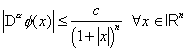

bottom:.0001pt\'>Es ist  D  ein Teilraum von  F , genauer liegt  D  dicht in  F . Stetige lineare Funktionale auf  F  heissen temperierte Distributionen. Diese benötigt man für die Fourier-Transformation: Für Funktionen  existiert die Fouriertransformierte  F [f(x)](p) definiert als

bottom:.0001pt\'> .

bottom:.0001pt\'>Analog zu den obigen Definitionen wird die Fourier-Transformierte von temperierten Distributionen T über die Fourier-Transformierte der Testfunktion definiert:

bottom:.0001pt\'>.

bottom:.0001pt\'>Mit geeigneten "Fortsetzungen" für einige Distributionen aus D\' in S\' kann man für diese ebenfalls eine Fourier-Transformation erklären. Auf diese Weise erhält man eine wichtige Fourier-Darstellung der d-Distribution

bottom:.0001pt\'>

bottom:.0001pt\'>und für beliebige Ableitungen  der d-Distribution gilt

bottom:.0001pt\'>

bottom:.0001pt\'>Das Konzept der verallgemeinerten Funktionen als Funktionale auf Testfunktionenräumen erlaubt eine mathematisch präzise Beschreibung von Quantenfeldern. Weil diese als Funktionen eines Punktes x des Minkowski-Raumes in der Form f(x) keine wirkliche Observable darstellen können - dies erforderte unendlich hohe Energie -, erscheint es sinnvoll, nur einen "gemittelten" Wert über eine hinreichend kleine Umgebung des Punktes als messbare Grösse zu betrachten. Man definiert daher Quantenfelder als operatorwertige Distributionen auf dem Minkowski-Raum, d.h. man verwendet in Matrixelementen der Form  das Quantenfeld f als ein mit einer Testfunktion f "verschmiertes" Quantenfeld . Ein anderes Beispiel für das Auftreten der Distributionen-Theorie in der Physik findet man im Rahmen der elementaren Quantenmechanik bei der Lösung der Schrödinger-Gleichung: Die zur Lösung dieser Gleichung benutzten ebenen Wellen e^ikx gehören gerade nicht zu den zulässigen Lösungsvektoren im HilbertRaum, nämlich den quadratintegrablen Funktionen. (Das Integral einer Funktion, die, wie z.B. e^ikx, auf dem ganzen Raum vom Betrag 1 ist, divergiert.) Auch diese Problematik wird mathematisch konsistent mit Hilfe von Gelfand-Tripeln, also innerhalb der Theorie der Distributionen gelöst.

bottom:.0001pt\'>Somit zeigt sich, dass nicht nur in der "klassischen" Einführung der d-Distribution als Dichtefunktion einer Punktladung, sondern auch in der Feldtheorie oder der Quantenmechanik Distributionen vertraute physikalische Idealisierungen mathematisch exakt abbilden.

bottom:.0001pt\'>Die d-Distribution wurde formal 1925 als Punktdichtefunktion mit geeigneten Rechenregeln, welche die Besonderheiten dieses Konstrukts berücksichtigten, von P.A.M. Dirac eingeführt. S.L. Sobolew (1908-1989) benutzte 1936 verallgemeinerte Funktionen im heutigen mathematischen Sinn zur Lösung des Cauchy-Problems für hyperbolische Differentialgleichungen. Die vollständige Theorie wurde in der zweiten Hälfte der vierziger Jahre vom französischen Mathematiker L. Schwartz (geb. 1915) entwickelt und in einer Monographie [1] niedergelegt. Eine umfassende Darstellung einschliesslich der Gelfand-Tripel bieten die vier Bände von Gelfand, Schilow und Wilenkin [2], [3]. Kurze Einführungen bieten [4] und [5]. Als gutes deutsches Standardwerk kann [6] gelten; Anwendungen der Theorie der Distributionen im Bereich partieller Differentialgleichungen werden in [7] und im Bereich von Pseudodifferentialoperatoren in [8] dargestellt. [9] enthält eine kurze Darstellung der Anwendung von operatorwertigen Distributionen in der relativistischen Quantenfeldtheorie.

Literatur
[1] Schwartz, L.: Théorie des Distributions. Herman, Paris 1966.
[2] Gelfand, I.M., Schilow, G. E.: Verallgemeinerte Funktionen (Distributionen), Bd I (1960), II (1962), III (1964) VEB Berlin.
[3] Gelfand, I.M., Wilenkin, N.J.: Verallgemeinerte Funktionen (Distributionen), Bd IV (1964).
[4] Constantinescu, F.: Distributionen und ihre Anwendung in der Physik, Teubner, Stuttgart 1974.
[5] Lighthill, M J: Einführung in die Theorie der Fourier-Analysis und der verallgemeinerten Funktionen, BI, Mannheim 1966.
[6] Jantscher, L.: Distributionen, de Gruyter, Berlin 1971.
[7] Wloka, J.: Partielle Differentialgleichungen, Teubner, Stuttgart 1982.
[8] Taylor, M. E.: Pseudodifferential Operators, Princeton UP, Princeton 1981.
[9] Streater, R. F., Wightman, A. S.: PCT, Spin, Statistics, and all that, Benjamin, Cummings, Reading 1964.