Techniklexikon

Variationsprinzip

Mathematische Methoden und Computereinsatz, ein in der theoretischen und mathematischen Physik aus naturphilosophischen Motivationen entwickeltes allgemeines Integralprinzip bzw. eine allgemeine Methode zur Aufstellung von Gleichungen zur Bestimmung von Funktionen, insbesondere Kurven oder Flächen. Man spricht von einem Prinzip, da man in sehr einheitlicher und formaler Weise (dieser Gedanke geht wesentlich auf P.L.M. Maupertuis zurück, der bemüht war, verschiedene Naturgesetze, die bislang als unvereinbar angesehen wurden, in Einklang zu bringen) versucht, eine differentielle Bedingung an eine Funktion bzw. Kurve aus der Forderung abzuleiten, dass eine bestimmte integrale Grösse, z.B. die Energie, die Wirkung, die Zeit oder die durchlaufene Weglänge, minimiert wird. Diese differentielle Bedingung gewinnt man in der Variationsrechnung aus der Variation von Funktionen bzw. Kurven einer bestimmten Funktionenklasse. Das bekannteste Beispiel ist das Hamiltonsche Prinzip (ursprünglich von Maupertuis entwickelt und auch Prinzip der kleinsten Wirkung genannt; korrekterweise müsste es Prinzip der stationären Wirkung heissen, da durch die notwendige Bedingung der Stationarität möglicherweise auch Sattelpunkte und Maxima erfasst werden) aus der klassischen Mechanik, das für Punktsysteme verlangt, dass der Übergang von einem Zustand in einen anderen in dem vorgegebenem Zeitintervall  so geschieht, dass die erste Variation  des Funktionals

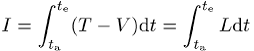
verschwindet () bzw. das Wirkungsintegral  (man beachte, dass [I] = Energie ´ Zeit) minimal bzw. stationär wird;  heisst Lagrange-Funktion. Mit Hilfe der Methoden der Variationsrechnung leiten sich daraus die Euler-Lagrange-Gleichungen ab. Weitere Beispiele für Variationsprinzipe sind in der Optik das Prinzip der kürzesten Zeit (bzw. des kürzesten optischen Weges) , wobei  den Brechungsindex,  das Bogenelement und  und  Ausgangs- und Endpunkt des Lichtstrahls bezeichnen. Dieses Prinzip wurde von Hamilton in mathematischer Strenge als Variationsprinzip formuliert, hat aber bereits Vorläufer in Heron von Alexandria im 1. Jahrhundert, der es für die Reflexion, und in P. de Fermat, der es 1662 in seinem Fermatschen Prinzip für die Refraktion aufstellt; Maupertuis bringt mit seiner Arbeit »Der Einklang verschiedener Naturgesetze, die bislang als unvereinbar angesehen wurden« die Extremalprinzipien der Optik und der Mechanik in Beziehung. In der Quantenmechanik mit Hamilton-Operator  führt das Ritzsche Variationsprinzip

auf die Eigenwertgleichung  zur Bestimmung der Wellenfunktion . In der Speziellen Relativitätstheorie wird ein speziell-relativistisch invariantes Wirkungsintegral variiert, und in der Allgemeinen Relativitätstheorie ist , wobei  das Riemannsche Bogenelement bezeichnet und somit sich der Körper auf einer Geodäten, der kürzesten Verbindung in der vierdimensionalen Raumzeit, bewegt. Schliesslich beruhen sämtliche Feldtheorien der Physik in Elektromagnetismus, Mechanik der Fluide oder Kontinua auf einem Variationsprinzip, wobei statt der Lagrange-Funktion eine passend gewählte Lagrange-Dichte  gewählt wird und das Wirkungsintegral  mit  eine allgemeinere Form annimmt. Variationsprinzipe repräsentieren den physikalischen Gehalt in einer sehr kompakten und einheitlichen Form und gestatten in einfacher Weise, die Invarianz gegenüber bestimmten Transformationen (Noether-Theorem) und damit die Existenz von Erhaltungssätzen nachzuweisen; sie erlauben elegant den Übergang zu anderen Koordinatensystemen, bilden häufig den Ausgangspunkt zur Konstruktion numerischer Verfahren und erfreuen sich als Extremalprinzipien auch grundlegender naturphilosphischer Bedeutung.