Techniklexikon

Hartree-Fock-Näherung

Atom- und Molekülphysik, Hartree-Fock-Verfahren, quantenmechanisches Näherungsverfahren zur Bestimmung der Wellenfunktionen und Energieniveaus bei mehreren identischen Fermionen, insbesondere Elektronen im Atom oder im Festkörper. Ursprünglich wurde das Hartree-Fock-Verfahren zur genaueren theoretischen Behandlung der Struktur der Atomhülle entwickelt. Es wurde von Hartree zunächst ohne, von Fock dann mit Berücksichtigung des Elektronenspins und der Austauschwechselwirkung formuliert. Nach dem Modell unabhängiger Teilchen besteht die Grundannahme in der Existenz von Einelektronen-Wellenfunktionen, wobei die entsprechenden Zustände unter Beachtung des Pauli-Prinzips besetzt werden. Dabei wird die Wellenfunktion eines beliebig herausgegriffenen Elektrons als Lösung einer Schrödinger-Gleichung bestimmt, in der Wechselwirkungen mit den anderen Elektronen durch ein mittleres Potential approximiert werden. Diese Grundidee, nämlich der Ersatz der Wechselwirkung zwischen den Elektronen durch ein Einteilchenpotential, ist schon im Rahmen der älteren Quantentheorie erfolgreich erprobt worden (Abschirmung).

Die Gesamtfunktion wird als Produkt (Hartree) y(1, ..., N) = j₁(1)j₂(2) ...j_N(N) bzw. als antisymmetrisiertes Produkt (Fock)

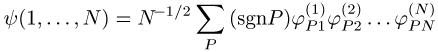
geschrieben, die Summation läuft über alle Permutationen P(1, 2, ..., N) = (Pl, P2, ..., PN) der Zahlen 1 ... N, sgn P ist das Vorzeichen der Permutation P, N ist die Teilchenzahl. Dabei kann die antisymmetrische Wellenfunktion auch in der Form der Slater-Determinante

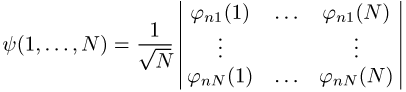
formuliert werden. Im Argument der Einteilchenwellenfunktionen sind der Ortsvektor r_k und die Spinvariable s_k zusammenfassend mit k bezeichnet. Die Spinvariable s_k kann nur die Werte ±1 / 2 annehmen. Bei Vernachlässigung magnetischer Wechselwirkungen können die  als Produkte aus je einer nur von der Ortskoordinate r_k abhängigen und einer nur von der Spinvariablen s_k abhängigen Funktion angesetzt werden: . Für die Spinfunktionen  könnte man etwa eine Darstellung durch ein Kronecker-Symbol  wählen. Bestimmungsgleichungen für die Einteilchenwellenfunktionen erhält man aus der Extremaleigenschaft der Energie  mit dem Vielelektronen-Hamilton-Operator

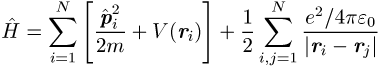
eines nichtrelativistischen Elektronensystems, wobei die  variiert werden. Mit dem gegenüber Teilchenzahlvertauschungen antisymmetrischen Hartree-Fock-Ansatz erhält man das folgende nichtlineare System von Integrodifferentialgleichungen zur Berechnung der Einteilchenwellenfunktionen :

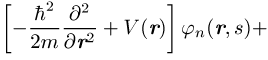
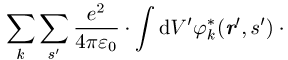
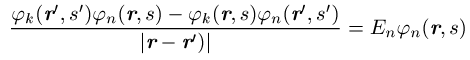
Die Integration erstreckt sich über den ganzen Raum und die s¢-Summe über die Werte ±1 / 2 der Spinvariablen. Die k-Summe umfasst alle besetzten Einteilchenzustände. Berücksichtigt man, dass die Summation über s¢ für ein Produkt j_n(r¢, s¢)j_m(r¢, s¢) stets null liefert, wenn die Spins beider Zustände nicht übereinstimmen, so ergibt sich folgendes: Das effektive Potential in den Gleichungen des Hartree-Fock-Verfahrens besteht zunächst wie beim Hartree-Verfahren aus dem Potential V(r), das auf jedes einzelne Elektron wirkt und das bei einzelnen Atomen gleich dem Coulomb-Potential -Ze² / 4pe₀r des Z-fach geladenen Kerns, bei Kristallen gleich der gitterperiodischen Überlagerung der Potentiale aller Ionenrümpfe ist, und dem Potential, das alle anderen Elektronen im Mittel erzeugen. Der Beitrag der Elektronen, deren Spinrichtung mit der des Zustandes j_n übereinstimmt, zum effektiven Potential wird durch den Austauschterm korrigiert. Der Austauschterm beruht auf der Korrelation der Elektronen infolge der Antisymmetrie der Wellenfunktion; er tritt bei dem einfachen Hartreeschen Produktansatz nicht auf und berücksichtigt ein zusätzliches gegenseitiges Ausweichen der Elektronen gleichen Spins. Nach dem Koopmansschen Theorem kann E als diejenige Energie interpretiert werden, die man aufwenden muss, um ein im Zustand j_n befindliches Elektron aus dem System zu entfernen.

Bei Anwendung auf Atome werden die Einteilchenwellenfunktionen  im Atom durch die Hauptquantenzahl n, die Drehimpulsquantenzahlen l und m_l sowie die Spinquantenzahl m_s charakterisiert.

Die über die Berechnung einer Elektronenkonfiguration bei nichtabgeschlossenen Elektronenschalen bzw. Unterschalen auftretende Feinstruktur kann nicht mit einer einzigen Slater-Determinante erfasst werden.

Das dem Austauschterm entsprechende Austauschpotential ist nichtlokal und erschwert die Lösung des Hartree-Fock-Verfahrens beträchtlich. In Festkörpern mit ihren vielen Elektronen wird es daher stets lokal approximiert (Slater-Methode). In dem so entstehenden Potential können auch über das Hartree-Fock-Verfahren hinausgehende Korrelationseffekte berücksichtigt werden (Dichtefunktionaltheorie).

Für ein freies Elektronengas mit einem homogenen »Untergrund« positiver Ladungen geben sich in Hartreescher Näherung, also bei völliger Vernachlässigung des Austauschterms, die Energien zu , während das Hartree-Fock-Verfahren einen Zusatzterm liefert, der an der Fermi-Fläche eine logarithmisch divergente Ableitung hat, d.h. die Fermi-Geschwindigkeit divergiert in Hartree-Fock-Näherung, und die Zustandsdichte N(E_F) an der Fermi-Energie verschwindet. Dieses anomale Verhalten tritt bei lokaler Approximation des Austauschterms (Slater-Methode) nicht auf. Bei einfachen Metallen ist dann der Einfluss des Austauschpotentials auf die Energien E(k) wegen der räumlich nahezu homogenen Valenzelektronendichte gering. Bei Halbleitern und Übergangsmetallen ergibt die Berücksichtigung des Austauschpotentials jedoch eine bedeutende Verbesserung des Energiespektrums, verglichen mit Hartree-Rechnungen. Konkrete Rechnungen mit dem Hartree-Fock-Verfahren sind sehr aufwendig, auf iterativem Weg wird eine selbstkonsistente Lösung bestimmt (self-consistent field).