Techniklexikon

Zentralbewegung

Klassische Mechanik, Bewegung eines Massenpunktes oder Körpers unter dem Einfluss einer Kraft, die immer auf denselben Punkt im Raum, das Zentrum 0, oder von diesem weg zeigt (siehe Abb.). Diese beschleunigende Kraft heisst Zentralkraft und bewirkt eine Beschleunigung, die ebenfalls immer auf das Zentrum 0 oder von diesem weg weist. Der Punkt 0 heisst Bewegungs- oder Beschleunigungszentrum und wird bei der Beschreibung der Bewegung üblicherweise als Ursprung des Koordiantensystems definiert. Jede Zentralkraft definiert ein Zentralkraftfeld oder Zentralfeld , wobei der Vektor r der vom Zentrum 0 zum Körper gerichtete Radiusvektor mit Betrag r,  die Geschwindigkeit des Körpers und t die Zeit ist. Die Verbindungsstrecke zwischen dem Beschleunigungszentrum und dem sich bewegenden Körper wird als Fahrstrahl bezeichnet. Dieser überstreicht bei jeder Zentralbewegung in gleichen Zeiten gleich grosse Flächen. Dieser Flächensatz (zweites Keplersches Gesetz) ist eine spezielle Form des Drehimpulserhaltungssatzes, der für alle Zentralbewegungen gilt: Der Drehimpuls L ist konstant, da seine zeitliche Ableitung, das Drehmoment , wegen  Null ist. Eine Zentralbewegung ist somit stets eben und erfolgt in der zu L senkrecht stehenden Ebene, die durch die Vektoren r₀, den Anfangsort, und v₀, die Anfangsgeschwindigkeit, aufgespannt wird. Die Bewegungsgleichungen in ebenen Polarkoordinaten in einem Zentralkraftfeld lauten:

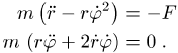
Die zweite Gleichung ist äquivalent zu , was wegen  der schon erwähnten Drehimpulserhaltung entspricht. Mit  ergibt sich wegen  der Flächensatz . Mit Hilfe der aus dem Flächensatz folgenden Beziehung  folgt aus der ersten Bewegungsgleichung die Binetsche Formel

aus der man bei bekannter Bahnkurve  die wirkende Kraft ermitteln kann. Auf diese Weise gelang Newton die Ableitung des Gravitationsgesetzes aus dem zweiten Keplerschen Gesetz.

Die Zentralbewegung verläuft stets krummlinig, kann aber sowohl gleichförmig (Betrag der Geschwindigkeit ist konstant) als auch ungleichförmig sein. Beispiele sind die gleichförmige und die gleichmässig beschleunigte Kreisbewegung, die Bewegung unter dem Einfluss der Gravitationskraft, die immer auf den Massenmittelpunkt des Systems aus Körpern oder Massenpunkten gerichtet ist (Planetenbewegung um die Sonne bzw. Mondbewegung um den Planeten) oder die Bewegung unter dem Einfluss der Coulomb-Kraft, die stets zum Ladungsschwerpunkt weist.

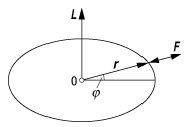
Zentralbewegung: Die ebene Bewegung um das Zentrum 0 wird durch die Kraft F hervorgerufen, die stets zum Punkt 0 zeigt oder von ihm weg weist, die also immer parallel zum Ortsvektor r ist. Der Drehimpuls L ist konstant und steht senkrecht auf der Bewegungsebene. In ebenen Polarkoordinaten (r, j) können die Bewegungsgleichungen gelöst werden.