Techniklexikon

Tensoranalysis

Mathematische Methoden und Computereinsatz, Teildisziplin der Mathematik bzw. der mathematischen Physik, die sich mit Tensorfeldern und insbesondere mit der Differentiation und Integration von Tensoren befasst und diese mit Hilfe der Differentialrechnung und Integralrechnung untersucht. Die Tensorgleichungen der Physik, bspw. die der Elektrodynamik und der Allgemeinen Relativitätstheorie, sind so gebaut, dass sie die Naturgesetze unabhängig vom Koordinatensystem beschreiben (Kovarianz). Eine wichtige Rolle spielt hierbei die kovariante Differentiation. Während die partiellen Ableitungen eines Tensors im allgemeinen nicht wieder auf einen Tensor führen, ist die kovariante Ableitung eines Tensors wiederum ein Tensor. Die kovarianten Ableitungen der kontravarianten bzw. kovarianten Komponenten eines Tensors  sind als

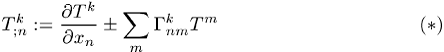
definiert, wobei  die Christoffel-Konnexion bezeichnet, die in folgender Weise vom kovarianten Metriktensor  (Koordinatensysteme) und vom kontravarianten Metriktensor , der aus der inversen Matrix von  hervorgeht, abhängt:

hierbei ist  als gewöhnliche Ableitung  zu lesen. Die kovariante Ableitung beliebiger Tensoren lässt sich berechnen, indem man  auf jeden kontra- bzw. kovarianten Index anwendet. Die kovariante Ableitung des Metrik- und Levi-Civita-Tensors ist Null, d.h. diese beiden Tensoren sind kovariant konstant. Die kovariante Ableitung ist eng verknüpft mit dem Konzept der Parallelität und Parallelverschiebung eines Vektorfeldes in einem nichteuklidischen Raum. Neben dem Metriktensor einer Fläche bzw. eines Raumes spielt in der Tensoranalysis und Allgemeinen Relativitätstheorie der Krümmungstensor, ein Tensor 4. Stufe,

eine wichtige Rolle. Vermöge der Christoffel-Symbole ist der Krümmungstensor mit den ersten und zweiten Ableitungen des Metriktensors verknüpft.