Techniklexikon

Schwingungen

Schwingungen und Wellen, Oszillationen, Vibrationen, zeitlich periodische Änderung einer oder mehrerer physikalischer Grössen um einen Mittelwert. Sie treten auf, wenn Störungen mechanischer, elektrischer oder auch thermischer Gleichgewichte zu Kräften führen, die der Störung entgegenwirken. Bei mechanischen Schwingungen kann die schwingende Grösse z.B. eine aus ihrer Ruhelage ausgelenkte Masse (Pendel, Stimmgabel, Membran, Saite usw.) sein (Saitenschwingungen, Stabschwingungen, Pendel). Bei elektromagnetischen Schwingungen sind die elektrische und magnetische Feldstärke, die elektrische Ladung eines Kondensators, die Stromstärke, die Spannung usw. die periodisch veränderlichen Grössen (Schwingkreis). Auch im Plasma treten Schwingungen auf, wenn die Quasineutralität durch Ladungsverschiebungen gestört wird (Plasmaschwingungen). Breitet sich eine Schwingung im Raum aus, so spricht man von Wellen.

Zu unterscheiden sind zunächst freie und erzwungene Schwingungen. Letztere werden durch eine periodische äussere Kraft zum Schwingen gebracht, während bei ersteren nur innere Kräfte wirken. Bei Anwesenheit dissipativer Prozesse (z.B. Reibung) spricht man von gedämpften Schwingungen. Die Eigenschaften des Systems hängen dann ganz entscheidend von der relativen Stärke der Dämpfung ab.

Ist das Differentialgleichungssystem für die schwingungsfähigen Variablen  linear, handelt es sich um lineare Schwingungen. Für solche Gleichungssysteme existieren allgemeine mathematische Lösungsverfahren. Dies ist von besonderer Bedeutung, da Schwingungen mit verhältnismässig kleiner Amplitude meist näherungsweise durch lineare Schwingungen beschrieben werden können, indem, ausgehend von der Gleichgewichtslage , die Taylor-Entwicklung der rückstellenden Kraft nach dem linearen Term abgebrochen wird (Schwingungen, kleine). Schwieriger ist dagegen die Behandlung von nichtlinearen Schwingungen. Trotz ihrer grossen praktischen Bedeutung (viele periodische physikalische Vorgänge sind nur in erster Näherung für kleine Amplituden durch ein lineares Gleichungssystem zu beschreiben) existieren nur für einige wenige Spezialfälle allgemeine mathematischen Lösungsverfahren.

Unter harmonischen Schwingungen versteht man Schwingungen mit einem sinusförmigen Schwingungsverlauf. Voraussetzung dafür ist eine der Auslenkung proportionale rückstellende Kraft. Bei gekoppelten Systemen führt dies zu einem linearen Differentialgleichungssystem – es handelt sich also um lineare Schwingungen. Umgekehrt sind jedoch nicht alle linearen Schwingungen auch harmonisch, etwa bei linearer Dämpfung. Die meisten Schwingungen sind anharmonisch und ihr Verlauf ist häufig eine sehr komplizierte periodische Funktion der Zeit. Diese kann jedoch in eine harmonische Grundschwingung und eine im allgemeinen grosse Anzahl von harmonischen Oberschwingungen zerlegt werden, deren Frequenzen ganzzahlige Vielfache der Grundfrequenz sind (Fourier-Reihe). Anharmonische Schwingungen liegen bei nahezu allen realen Systemen mit grosser Amplitude vor, wie z.B. auch dem Fadenpendel (Pendel). Weitere Beispiele für anharmonische Schwingungen sind Kippschwingungen oder Töne, die erst durch die charakteristische Verteilung der Obertöne ihre typische Klangfarbe erhalten.

Die mathematische Behandlung von Schwingungen führt unabhängig von der genauen Problemstellung häufig auf formal identische Differentialgleichungen. Die wichtigsten Grundtypen sollen hier am Beispiel des Federpendels vorgestellt werden.

Für eine Masse  und eine Richtgrösse (Federkonstante)  lautet die Schwingungsgleichung für die Auslenkung  aus der Ruhelage:

Es handelt sich um ein lineares Gleichungssystem. Durch Integration erhält man als Lösung harmonische Schwingungen

mit .  ist die Amplitude,  die Kreisfrequenz und  die Schwingungsdauer oder Periode der Schwingung. Darüber hinaus bezeichnet  die Phasenverschiebung, die bei geeigneter Wahl der Zeitskala Null gesetzt werden kann und  die Frequenz.

Durch Einführung eines energieverzehrenden Prozesses (Reibung) erhält man gedämpfte Schwingungen. Häufig ist diese Reibungskraft proportional zur Geschwindigkeit . Mit der Dämpfungskonstanten  und der Abkürzung  gelangt man zu folgender linearer Schwingungsgleichung:

Bei der Lösung sind drei Fälle zu unterscheiden: Im Schwingfall mit  erhält man gedämpfte harmonische Schwingungen mit abnehmender Periode (siehe Abb. 1):

wobei . Die Grösse  heisst logarithmisches Dekrement und ist ein Mass für Abnahme der Amplitude pro Schwingungsperiode :

und damit der zu  proportionalen in der Schwingung gespeicherten Schwingungsenergie.

Für starke Dämpfung  wird der Vorgang aperiodisch: die Grösse  nähert sich von einer Seite her asymptotisch dem ungestörten Gleichgewichtszustand. Deshalb spricht man auch vom Kriechfall. Die Lösung setzt sich dabei aus zwei exponentiellen Termen zusammen:

mit  und entsprechend gewählten Parametern  und .

Technisch ist der aperiodische Grenzfall mit  (mittlere Dämpfung) von besonderer Bedeutung, denn die Schwingung erreicht in diesem Fall die Ruhelage in der kürzest möglichen Zeit. Dies ist insbesondere bei Zeigermessgeräten, Stossdämpfern usw. erwünscht. Die Lösung setzt sich wieder aus zwei Termen zusammen:

Zu erzwungen Schwingungen gelangt man ausgehend von den eben behandelten freien Schwingungen durch Einführung einer äusseren Kraft , die zusätzlich zur rücktreibenden Kraft und der Reibungskraft periodisch auf das schwingungsfähige System einwirkt. Für  ergibt sich dann als Schwingungsgleichung

Die Lösung ist bei schwacher Dämpfung () die Überlagerung einer abklingenden Schwingung mit der Eigenfrequenz  des Systems (Einschwingvorgang) über einem stationären Vorgang der Form . Die Phasendifferenz  zwischen einwirkender Kraft und der ausgeführten Schwingung berechnet sich zu  und für die Amplitude  gilt (siehe Abb. 2+3):

Das System schwingt also mit der Frequenz der anregenden Kraft. Ist diese Frequenz sehr viel kleiner als die Eigenfrequenz  des System, folgt es der äusseren Kraft ohne Phasenverschiebung. Bei sehr hohen Frequenzen schwingen das System und die äussere Kraft hingegen gegenphasig und im Bereich der Resonanz () beträgt die Phasenverschiebung genau . Der Energieübertrag ist dann maximal und die Amplitude nimmt sehr grosse Werte an, die sogar zur Zerstörung des Geräts führen können (Resonanzkatastrophe). Das Maximum der Amplitude (Amplitudenresonanz) wird mit Dämpfung für  erreicht, das Maximum der kinetischen Energie (Energie- oder Geschwindigkeitsresonanz) für . (Saitenschwingungen)

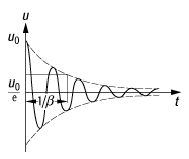
Schwingungen 1: Amplitudenverlauf einer gedämpften freien Schwingung (Schwingfall).

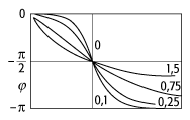
Schwingungen 2: Phasenverschiebung zwischen erregender Kraft und Schwingung für verschiedene Werte der relativen Dämpfung . Bei langsamer Anregung folgt das System der äusseren Kraft, bei schneller Anregung schwingt es gegenphasig und im Resonanzfall () beträgt die Verschiebung genau .

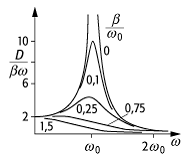
Schwingungen 3: Amplitude einer erzwungenen Schwingung (nach dem Einschwingvorgang). Ohne Dämpfung () steigt die Amplitude bei  ins Unermessliche (Resonanzkatastrophe).