Techniklexikon

Pendel

Schwingungen und Wellen, in einem homogenen Kraftfeld meist um eine feste Achse (ebenes Pendel) oder um einen festen Punkt (räumliches Pendel) drehbar gelagerter starrer Körper, der unter dem Einfluss dieser Kraft Schwingungen um eine Ruhelage ausführt. Finden diese Schwingungen unter dem Einfluss des Schwerefeldes statt, so spricht man von einem Schwerependel.

Ein Pendel, das im Grenzfall aus einem Massepunkt und einem gewichtslosen Aufhängefaden besteht, heisst mathematisches Pendel, im Gegensatz zum physikalischen Pendel, bei dem der Pendelkörper eine beliebige Masseverteilung besitzen kann.  Das mathematische Pendel wird in der Praxis sehr gut durch ein Fadenpendel angenähert: ein kleiner aber schwerer Körper, der am Ende eines langen dünnen Fadens aufgehängt ist. Im einzelnen unterscheidet man:

1) Ausgleichspendel, Minimalpendel, physikalisches Pendel (siehe 28) in einer Form, bei der z.B. durch Temperaturschwankungen verursachte Änderungen der Pendellänge den geringsten Einfluss auf die Schwingungsdauer haben. Da die Schwingungsdauer des physikalischen Pendels von seiner reduzierten Pendellänge  abhängt, darf diese sich beim Ausgleichspendel bei kleinen Änderungen des Abstandes  des Schwerpunktes von der Drehachse nur minimal ändern. Dies führt auf die Bedingung . Für die reduzierte Pendellänge gilt die Beziehung

denn nach dem Steinerschen Satz kann das auf die Drehachse bezogene Trägheitsmoment  als  geschrieben werden (: das auf die zur Drehachse parallelen Schwerpunktsachse bezogene Trägheitsmoment, : Pendelmasse und : Trägheitsradius). Aus  folgt dann  und .

Unter Verwendung von Ausgleichspendeln wurden die genauesten astronomischen Pendeluhren gebaut, bei denen ein solches Pendel, elektromagnetisch angetrieben, in verdünntem Wasserstoff schwingt.

2) ballistisches Pendel, Stosspendel, ein Schwerependel, das durch einen Kraftstoss aus der Ruhelage ausgelenkt wird. Wählt man als Pendelkörper ein plastisches Material, so lässt sich das Pendel zur einfachen Messung von Geschwindigkeiten einsetzen, insbesondere der von Geschossen.

Meist besteht das ballistische Pendel aus einer einseitig offenen, mit Sand gefüllten Kiste, die an einer horizontalen Achse aufgehängt ist. Das Geschoss bleibt im Sand stecken (unelastischer Stoss) und überträgt seinen Impuls auf das Pendel, wodurch dieses einen Drehimpuls erhält. Die Geschwindigkeit  eines Geschosses der Masse  kann aus der maximalen Auslenkung  und dem Abstand  des Einschlagspunktes von der Achse aus

berechnet werden. Dabei ist  die Gesamtmasse des Pendels,  das Trägheitsmoment des Pendels bezüglich seiner Drehachse,  der Abstand des Pendelschwerpunktes von der Drehachse und  die Erdbeschleunigung.

3) Bifilarpendel, in der Seismometrie verwendetes Pendel.

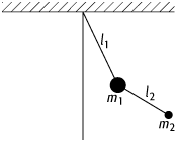
4) Doppelpendel, eine Pendelanordnung, bei der an einem ersten Pendel der Masse  und der Länge  ein zweites Pendel der Masse  und der Länge  hängt (siehe Abb. 1). Die genaue mathematische Behandlung eines Doppelpendels ist sehr kompliziert. Für kleine Auslenkungen kann man wie beim mathematischen Pendel  durch  ersetzen, und es ergibt sich, dass die beiden Pendel auf keinen Fall mit genau derselben Frequenz schwingen können.

Fast übereinstimmende Frequenzen ergeben sich für  und . Gibt man dem oberen Pendel einen kurzen Stoss, gerät das untere in lebhafte Bewegungen, während das obere zur Ruhe kommt. Das untere Pendel beruhigt sich schliesslich wieder und das obere schlägt wieder stärker aus, usw. Die Energie wandert also zwischen den beiden Pendeln hin und her, es treten Schwebungen auf.

5) Drehpendel, Torsionspendel (siehe 42).

6) ebenes mathematisches Pendel, mathematisches Pendel (siehe 24), dessen Schwingung auf eine vertikale Ebene beschränkt ist.

7) Elementarpendel, Bezeichnung für eine Kugel zwischen zwei gespannten Schraubenfedern als experimentelle Realisierung eines harmonischen Oszillators.

8) Fadenpendel, ein Pendel, bei dem eine kleine Kugel aus einem schweren Material an einem langen dünnen Faden hängt. Das Fadenpendel realisiert weitgehend das mathematische Pendel (siehe 24). Die sehr geringen Abweichungen seiner Schwingungsdauer von derjenigen des mathematischen Pendels bei kleinen Auslenkungen () wegen der endlichen Ausdehnung der Pendelmasse und des Einflusses der Fadenmasse ist durch folgende Formel gegeben:

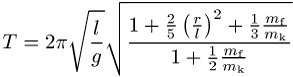
( und : Faden- bzw. Kugelmasse (), : Kugelradius, : Pendellänge bis zum Kugelmittelpunkt (), : Schwerebeschleunigung).

Mit Hilfe dieser Formel kann auch das Fadenpendel zur Bestimmung der Erdbeschleunigung  aus der Schwingungsdauer benutzt werden, jedoch wird für wissenschaftliche Zwecke meistens das Reversionspendel (siehe 31) verwendet.

9) Faradaysches Pendel, stabförmiges, leitendes Kegelpendel, das ganz leicht in ein Quecksilberbad eintaucht, in dessen Mitte ein senkrecht angebrachter Stabmagnet endet. Durchfliesst ein Strom von einigen Ampere das Pendel, so beginnt es, um den Magnetpol zu rotieren. Dies kann erklärt werden, wenn man die Überlagerung der Magnetfeldlinien, die den Strom kreisförmig umgeben, mit den radial vom Magnetpol ausgehenden Linien betrachtet. Vor dem Pendel entsteht eine Abschwächung, hinter dem Pendel eine Verstärkung des Feldes, wodurch die bewegende Kraft zustande kommt.

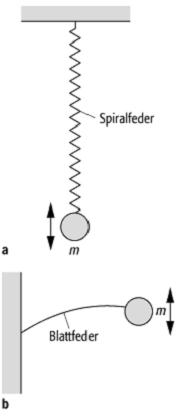
10) Federpendel, an einer Spiralfeder oder einer Blattfeder aufgehängte Masse, die unter der Einwirkung der Schwerkraft oder einer vertikalen Bodenbeschleunigung Schwingungen ausführt (siehe Abb. 2). Im ersten Fall dient es als grundsätzlicher Bestandteil von statischen Schweremessern (Gravimeter), im zweiten von Vertikalseismometern (Seismometrie). Für kleine Auslenkungen  aus der Ruhelage gilt nach dem Hookeschen Gesetz mit der Federkonstante  die Bewegungsgleichung  (in der schwingenden Masse  ist noch die halbe Federmasse enthalten), woraus die Schwingungsdauer  folgt.

11) Foucaultsches Pendel, Kamerlingh-Onnes-Pendel, gyroskopisches Pendel, Pendel zum Nachweis der Erdrotation (gyroskopische Bewegung) und damit dafür, dass die Erde kein Inertialsystem darstellt. Als Folge der in rotierenden Bezugssystemen auftretenden Corioliskraft beobachtet man eine langsame Drehung der Schwingungsebene eines mathematischen Pendels mit grosser Schwingungsdauer .

Diese Drehung hängt von der geographischen Breite des Ortes ab: an den Polen dreht sich die Erde unter der Schwingungsebene weg, d.h. ein Beobachter stellt bei einem vollen Hin- und Hergang des Pendels relativ zur Erde eine Drehung der Schwingungsebene um den Winkel  fest, wobei  die Winkelgeschwindigkeit der Erde ist. Am Äquator findet keine Drehung statt, das Pendel schwingt stets in der einmal vorgegebenen Ebene. Bei gegebener geographischer Breite  ist .

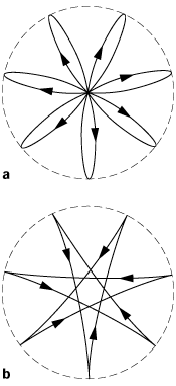
Der Pendelkörper beschreibt auf die Tangentialebene an die Erde projiziert, d.h. für den Beobachter im Laboratorium, eine Rosettenbahn mit Schleifen, wenn die Schwingung durch Anstossen aus der Ruhelage, oder mit Spitzen, wenn sie durch Loslassen des Pendels aus der Lage maximaler Auslenkung beginnt (siehe Abb. 3).

Im historischen Versuch im Pariser Pantheon 1851 benutzte Foucault eine Pendelmasse von 28 kg an einem 67 m langen Faden. Tatsächlich wurde der Versuch jedoch erstmals bereits im Jahre 1661 von Viviani durchgeführt. Kamerlingh Onnes untersuchte 1879 in seiner Dissertation quantitativ alle Fehlerquellen des Foucaultschen Pendels und führte Präzessionsmessungen der Erdrotation mit einem Fehler unter 0,5 % durch.

12) Galitzin-Pendel, ein Seismometer (Seismometrie), bei dem die zum Teil sehr kleine Pendelmasse eine Induktionsspule trägt, die beim Schwingen des Pendels an den Polen eines starken Dauermagneten vorbeigeführt wird und dadurch einen Strom induziert.

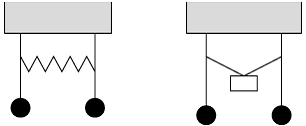
13) gekoppelte Pendel, sympathische Pendel, Pendel, die z.B. durch Federn oder auch durch Fäden, die mit Gewichten beschwert sind, verbunden und damit aneinandergekoppelt sind, so dass sie nicht mehr unabhängig voneinander schwingen (siehe Abb. 4). Bei zwei gekoppelten Pendeln gleicher Masse und gleicher Länge ergeben sich wie beim Doppelpendel (siehe 4), das die einfachste Form gekoppelter Pendel darstellt, Schwebungen: stösst man ein Pendel aus der Ruhe an, so wandert die Energie zwischen den beiden Pendeln hin und her, wobei abwechselnd das eine und das andere der beiden Pendel zur Ruhe kommt (oder bei leicht unterschiedlichen Pendeln zumindest annähernd zur Ruhe).

Bei  miteinander gekoppelten Pendeln gibt es genau  Fundamentalschwingungen (Schwingungen, kleine). Für die beiden Pendel, die durch eine Feder gekoppelt sind, gibt es also zwei Fundamentalschwingungen: Sie schwingen entweder in Phase oder (mit einer höheren Frequenz) gegenphasig. Die Bewegung der Pendel bei beliebigem Anstoss ergibt sich aus einer Überlagerung dieser Fundamentalschwingungen. Diese Überlagerung ist auch verantwortlich für die beobachteten Schwebungen.

14) gyroskopisches Pendel, Kamerlingh-Onnes-Pendel, Foucaultsches Pendel (siehe 11).

15) Horizontalpendel, in der Seismometrie verwendetes Pendel.

16) invariables Pendel, bei der Schweremessung (Gravimetrie) angewandter Begriff, um die mehr oder weniger gesicherte Unveränderlichkeit der Schwingungsdauer eines Pendels zu charakterisieren. Massgebend für die Invariabilität oder Konstanz des Pendels ist neben der Unveränderlichkeit der Länge und des Trägheitsmomentes auch die der Schneide und ihrer Auflage.

17) Invarpendel, Nickelstahl-Kompensationspendel, ein spezielles Kompensationspendel (siehe 20).

18) Kamerlingh-Onnes-Pendel, gyroskopisches   Pendel, Foucaultsches Pendel (siehe 11).

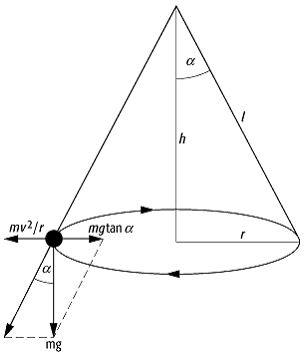
19) Kegelpendel, Kreispendel, konisches Pendel, mathematisches Pendel (siehe 24), dessen Bewegung nicht auf eine vertikale, sondern auf eine horizontale Ebene beschränkt ist. Die Pendelmasse läuft dann auf einem horizontalen Kreis mit gleichförmiger Geschwindigkeit um, wobei sich die masselos angenommene Pendelstange bzw. der Faden auf dem Mantel eines Kreiskegels mit vertikaler Achse bewegt (siehe Abb. 5). Wird die Bewegung des Pendels hingegen auf eine Kugeloberfläche beschränkt, spricht man von einem Kugelpendel ( siehe 23).

Zur Bestimmung der Umlaufdauer  betrachtet man das Kräftegleichgewicht zwischen der nach aussen wirkenden Zentrifugalkraft  und der nach innen wirkenden Komponente  der Gewichtskraft, woraus  folgt. Dabei ist  die Masse und  die Länge des Pendels,  der Öffnungswinkel des Kreiskegels,  dessen Radius und  die Schwerebeschleunigung.

Für kleine Winkel  ist , also  analog zum mathematischen Pendel bei kleinen Amplituden.

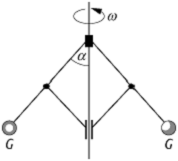
Das Kegelpendel wird in der Technik z.B. beim Fliehkraftregler eingesetzt: Zwei Kugeln hängen seitlich an der Drehachse herunter und ein Anwachsen der Winkelgeschwindigkeit führt zum Anheben der Massestücke , womit sich eine Regelung realisieren lässt (siehe Abb. 6). Man nennt diesen Pendeltyp deshalb auch Fliehkraft- oder Zentrifugalpendel.

20) Kompensationspendel, Pendel, bei dem sich die temperaturbedingten Längenänderungen der einzelnen Teile gegenseitig kompensieren, so dass die reduzierte Pendellänge und damit die Schwingungsdauer weitgehend konstant bleibt.

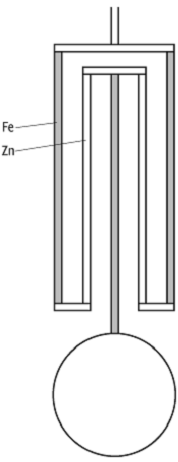
Beim Rostpendel wird z.B die Pendellinse von einer rostähnlich angeordneten Konstruktion aus Stahl- und Zink- oder Messingstäben getragen, deren Längenänderungen sich bei Temperaturschwankungen gegenseitig kompensieren (siehe Abb. 7).

Beim Quecksilber-Kompensationspendel dienen ein oder zwei Quecksilbergefässe als Pendellinse. Die Ausdehnung des Quecksilbers kompensiert hier die Längenänderung der Pendelstange.

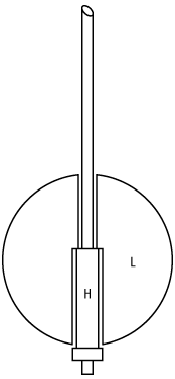
Die Pendelstange des Nickelstahl-Kompensationspendels von Riefler besteht aus Invar (Invarpendel), einer Nickelstahllegierung mit einem sehr niedrigen thermischen Ausdehnungskoeffizienten. Die Pendellinse L ruht auf einer Metallhülse H, die bei einer Temperaturerhöhung durch ihre Ausdehnung die Pendellinse etwas hebt und dadurch die Ausdehnung der Invarpendelstange gerade kompensiert (siehe Abb. 8).

21) konisches Pendel, Kreispendel, Kegelpendel (siehe 19).

22) Kreispendel, konisches Pendel, Kegelpendel (siehe 19).

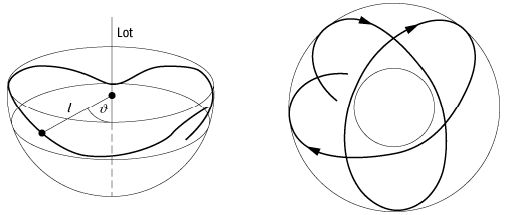
23) Kugelpendel, sphärisches Pendel, räumliches Pendel, allgemeine Form des mathematischen Pendels, bei der sich der Massepunkt auf einer Kugeloberfäche bewegen kann. Aus dem Energie- und Impulssatz folgt, dass die allgemeinste Bewegungsform des Massepunktes dann ein Pendeln zwischen zwei Breitenkreisen mit dem Azimut  bzw.  ist, von denen mindestens einer auf der unteren Halbkugel liegen muss (siehe Abb. 9). Die Bahnkurve hat keine Schleifen oder Spitzen, ist im allgemeinen nicht geschlossen und in der Draufsicht ergibt sich der in Abb. 9 skizzierte Bahnverlauf. Bei kleinen Ausschlägen bewegt sich der Massepunkt auf einer horizontalen Ellipse und seine Umlaufzeit beträgt näherungsweise  (: Pendellänge, : Schwerebeschleunigung). Ein Spezialfall des Kugelpendels stellt das Kegelpendel (siehe 19) dar, bei dem die Bewegung auf eine horizontale Ebene beschränkt ist.

24) mathematisches Pendel, idealisiertes Pendel, bei dem eine punktförmige Masse  durch eine starre und masselose Pendelstange der Länge  mit einem festen Punkt O verbunden ist und sich demnach nur auf einer Kugelfäche mit dem Radius  um den Punkt O bewegen kann (siehe 23, Kugelpendel). Diese Situation kann annähernd mit einem Fadenpendel (siehe 8) realisiert werden, wobei die Schwingungen jedoch auf die untere Halbkugel beschränkt werden müssen.

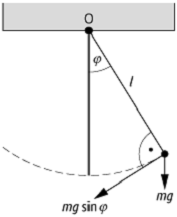
Wird die Bewegung des Pendels auf eine horizontale Ebene eingeschränkt, so dass die punktförmige Masse Kreisbahnen in dieser Ebene beschreibt, spricht man von einem Kreis- oder Kegelpendel (siehe 19). Bei einer Beschränkung der Bewegung auf eine vertikale Ebene durch den Punkt O, handelt es sich um ein ebenes mathematisches Pendel. Meist sagt man aber auch dann einfach nur »mathematisches Pendel«. Vernachlässigt man für diesen Fall die Reibung im Auflagepunkt O sowie den Luftwiderstand, so lautet die Pendelgleichung, also die Bewegungsgleichung des Massepunktes

mit , wobei  die Erdbeschleunigung und  die Länge des Pendels ist (siehe Abb. 10). Für kleine Ausschläge oder Amplituden lässt sich  durch  nähern, woraus sich die linearisierte Pendelgleichung

mit der allgemeinen Lösung

ergibt (: Amplitude, : Phasenkonstante). Die Schwingungsdauer  ist für relativ kleine Auslenkungen also weder von der Masse noch von der Amplitude abhängig, sondern nur von der Länge des Pendels. Beträgt die halbe Periode gerade eine Sekunde, so spricht man von einem Sekundenpendel.

Die Bestimmung der Schwingungsdauer aus der nicht linearisierten Pendelgleichung führt auf ein vollständiges elliptisches Integral der ersten Gattung, woraus sich die von der Amplitude  abhängende Periode  ergibt:

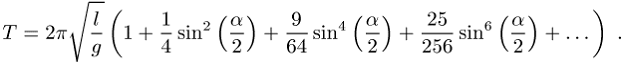
25) Minimalpendel, Ausgleichspendel (siehe 1).

26) Paraboloidpendel, ein Pendel, bei dem die Bewegung des Massepunktes auf die Oberfläche eines Rotationsparaboloids mit vertikaler Rotationsachse beschränkt ist. Im Gegensatz zum Kegelpendel (siehe 19), das eine Spezialform des Kugelpendels (siehe 23) darstellt, ist hier die Umlaufdauer auf einer horizontalen Kreisbahn unabhängig von ihrem Radius.

27) Parallelogrammpendel, wird ein Pendelkörper an zwei gleich langen parallelen Fäden aufgehängt, deren Masse vernachlässigbar klein ist, so ist seine Schwingungsdauer in der Ebene der Fäden gleich der einer Punktmasse, die an einem der beiden Fäden befestigt ist. Das Parallelogrammpendel stellt also eine einfache Verwirklichung des mathematischen Pendels (siehe 24) dar.

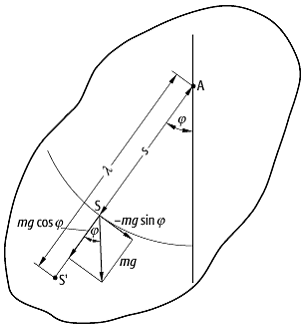
28) physikalisches Pendel, physisches Pendel, Bezeichnung für einen starren Körper beliebiger Form und Massenverteilung, der um eine horizontale Achse, die nicht durch seinen Schwerpunkt geht, unter dem Einfluss der Schwerkraft Schwingungen um seine Ruhelage ausführt.

Die auf das gesamte Pendel wirkende Schwerkraft kann zu einer Resultierenden zusammengefasst werden, die im Schwerpunkt S angreift. Wird das Pendel um den Winkel  aus der Ruhelage ausgelenkt (siehe Abb. 11), so übt die Schwerkraft  (: Pendelmasse, : Schwerebeschleunigung) das Drehmoment  aus (: Abstand des Schwerpunkts von der Drehachse A). Für die Schwingung um die Achse A ergibt sich die Bewegungsgleichung

(: Trägheitsmoment begzüglich der Achse A). Sie geht in die Differentialgleichung des mathematischen Pendels (siehe 24) über, wenn man die reduzierte Pendellänge  einführt. Ein physikalisches Pendel schwingt also genauso wie ein mathematisches mit der Pendellänge  und die für das mathematische Pendel gewonnenen Ergebnisse lassen sich auf das physikalische übertragen. Daher gilt z.B. für die Schwingungsdauer  bei kleinen Auslenkungen:

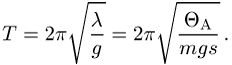
29) physisches Pendel, physikalisches Pendel (siehe 28).

30) räumliches Pendel, sphärisches Pendel,   Kugelpendel (siehe 23).

31) Reversionspendel, Pendel mit zwei einander zugekehrten Schneiden, bei dem es durch Verschieben von Gewichten oder auch der Schneiden möglich ist, die Massenverteilung so zu verändern, dass die Schwingungsdauer um beide Schneiden dieselbe ist (siehe Abb. 12). Da die reduzierte Pendellänge dann genau dem Abstand der beiden Schneiden entspricht, der sehr genau gemessen werden kann, ist es mit dem Reversionspendel möglich, die Erdbeschleunigung mit Hilfe der für das mathematische Pendel (siehe 24) hergeleiteten Formeln sehr genau zu bestimmen.

32) Riefler-Pendel, Bezeichnung für die beiden von Riefler konstruierten Kompensationspendel (siehe 20).

33) Rollpendel, Bezeichnung für einen Zylinder mit unsymmetrischer Massenverteilung, der unter der Wirkung der Schwerkraft auf einer horizontalen Unterlage rollend schwingen kann.

34) Rostpendel, Kompensationspendel (siehe 20).

35) Schwerependel, ein Pendel, das seine Schwingungen unter dem Einfluss des Schwerefeldes ausführt.

36) Sekundenpendel, Bezeichnung für ein Pendel, das für einen Hin- oder Hergang je eine Sekunde benötigt, dessen Schwingungsdauer  also zwei Sekunden beträgt. Mit der mittleren Erdbeschleunigung g = 9,81 m / s² ergibt sich die Länge des Sekundenpendels zu  cm (mathematisches Pendel, siehe 24). Auf Grund der unterschiedlichen Erdbeschleunigung beträgt seine Länge am Äquator 99,10 cm und an den Polen 99,63 cm.

37) Seismisches Pendel, Sammelname für alle Arten von Seismometerpendeln, d.h. von Pendeln, die den Hauptbestandteil von Seismometern bilden (Seismometrie).

38) stehendes Pendel, ein Pendel, dessen Schwerpunkt sich in der Ruhelage senkrecht über der Drehachse befindet. Zur Einhaltung der Nullage dient eine Blattfeder, deren Drehmoment  dem Drehmoment der Schwere  (jeweils für kleine Auslenkungen ) entgegenwirkt. Ist  sein Trägheitsmoment um die Drehachse, so beträgt die Schwingungsdauer

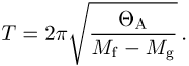
Da aus einer relativen Änderung der Schwingungsdauer auf eine Schwereänderung geschlossen werden kann, eignet sich dieses Pendel zur Ausführung relativer Schweremessungen.

39) Von-Sternecksches Pendel, von von Sterneck in die Geophysik eingeführtes Gerät zur Ausführung relativer Schweremessungen. Es ist in der ursprünglichen Form ein Halbsekundenpendel mit widerstandsarm geformter Pendelmasse und T-förmigem Schneidenträger. Der Pendelstab ist aus möglichst temperaturunempfindlichem Material, z.B. der Eisennickellegierung Invar (Kompensationspendel, siehe 20) hergestellt.

40) sphärisches Pendel, räumliches Pendel, Kugelpendel (siehe 23).

41) sympathische Pendel, gekoppelte Pendel (siehe 23).

42) Torsionspendel, Drehpendel, ein Pendel, bei dem nicht die Schwerkraft, sondern die Torsionselastizität einer Feder oder des Aufhängedrahtes die rücktreibende Kraft liefert. Diese ist innerhalb weiter Grenzen proportional zum Torsionswinkel und das Pendel führt daher harmonische Schwingungen aus.

43) Uhrenpendel, die in Pendeluhren zur Zeitmessung verwendeten Pendel, welche im allgemeinen als Kompensationspendel (siehe 20), bei astronomischen Uhren auch als Ausgleichspendel (siehe 1) konstruiert sind.

44) Waltenhofensches Pendel, Pendel zur Demonstration des Prinzips der Wirbelstrombremse.

45) Wiechert-Pendel, von E. Wiechert für seismologische Messungen konstruierte Pendel (Seismometrie).

46) Zeunersches Dreischneidenpendel, Pendel mit drei Schneiden, das die Bestimmung der Erdbeschleunigung  erlaubt, indem die Schwingungsdauer um jede der drei Schneiden einzeln gemessen wird.

47) Zweispitzenpendel, in der Seismometrie verwendetes Pendel.

48) Zykloidenpendel, Pendel, bei dem die Bewegung des Massenpunktes auf einer Zykloide verläuft. Während beim ebenen mathematischen Pendel (siehe 24) die Schwingungsdauer nur näherungsweise bei kleinen Auslenkungen unabhängig von der Amplitude ist, hat bereits Huygens gezeigt, dass die Schwingungsdauer unabhängig von der Amplitude wird, wenn sich der Massenpunkt statt auf einem Kreisbogen auf einer Zykloide bewegt. Deshalb wird diese mathematische Kurve auch Iso- oder Tautochrone genannt.

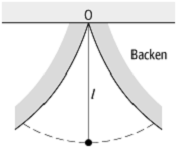
Die Führung eines Fadenpendels auf einer Zykloide lässt sich realisieren, indem man links und rechts vom Aufhängepunkt O zwei zykloidenförmige Backen anbringt (siehe Abb. 13), an die sich der Faden des Pendels bei seiner Schwingung anlegt. Eine solche Anordnung nennt man Huygens-Aufhängung oder tautochrone Aufhängung. Die Schwingungsdauer ist nun für beliebige Amplituden , wobei  die Länge des Pendels und  die Schwerebeschleunigung sind.

Pendel 1: Doppelpendel: an einem ersten Pendel der Länge  und der Masse  hängt ein zweites der Länge  und der Masse .

Pendel 2: Federpendel: Ausführung mit einer Spiralfeder (a) und einer Blattfeder (b).

Pendel 3: Foucaultsches Pendel: wird das Pendel aus der Ruhelage angestossen, so führt es auf Grund der Erdrotation Rosettenbahnen mit Schleifen durch (a), wird es aus der Lage maximaler Auslenkung losgelassen, Rosettenbahnen mit Spitzen (b).

Pendel 4: gekoppelte Pendel.

Pendel 5: Zur Geometrie des Kegelpendels.

Pendel 6: Kreispendel, das zur Drehzahlregelung eingesetzt werden kann (Fliehkraftpendel).

Pendel 7: Rostpendel: eine mögliche Ausführung eines Kompensationspendel.

Pendel 8: Nickelstahl-Kompensationspendel von Riefler.

Pendel 9: Kugelpendel: möglicher Bahnverlauf beim Kugelpendel in Perspektive (links) und Draufsicht (rechts).

Pendel 10: Mathematisches Pendel: Geometrie zur Herleitung der Pendelgleichung.

Pendel 11: Physikalisches Pendel: im Gegensatz zum mathematischen Pendel ist die Massenverteilung beliebig.

Pendel 12: Reversionspendel zur genauen Bestimmung der Erdbeschleunigung.

Pendel 13: Zykloidenpendel: Die Schnur legt sich an die zykloidenförmigen Backen an. Dadurch wird die Schwingungsperiode unabhängig von der Auslenkung.