Techniklexikon

Momente

Mathematische Methoden und Computereinsatz, 1) Statistik: skalare, aus Zufallsgrössen und Wahrscheinlichkeitsdichten berechnete Grössen, die in der Physik, insbesondere der Quantenphysik, häufig Anwendung finden. Das n-te Moment einer diskreten Zufallsgrösse x, die die Werte  mit den Wahrscheinlichkeiten  annehmen kann, ist definiert als

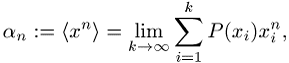
wenn die Reihe absolut konvergiert. Das kontinuierliche Analogon hierzu ist

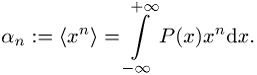
Das erste Moment, d.h. , wird auch Erwartungswert von  bezüglich  genannt. In praktischen Anwendungen wird man  durch  approximieren und nennt dies den Mittelwert; dies entspricht einer uniformen Dichte . Mit Hilfe des Moments lässt sich ferner das n-te zentrale Moment

definieren. In der Regel wird  betrachtet.  heisst Varianz; sie misst die Abweichung der Zufallsgrössen von ihrem Erwartungswert. Die zentralen Momente  und  tragen die Namen Schiefe (sie misst die Abweichung von der Symmetrie; in der Praxis oft die Abweichung von der Normalverteilung) und Bauchigkeit.  und  sind ihrerseits wiederum Zufallsgrössen.

2) Mechanik: Drehmoment, Trägheitsmoment, Flächenträgheitsmoment, Biegemoment.

3) Elektrodynamik: magnetisches Moment.