Techniklexikon

Hamiltonsches Prinzip

Prinzip der kleinsten Wirkung, allgemeines Prinzip, dessen Anwendungsbereich nicht auf die Mechanik beschränkt ist und das dynamische Verhalten physikalischer Systeme zu bestimmen ermöglicht. Die Bewegung eines mechanischen Systems von N Massepunkten kann als stetige Bahnkurve in einem mehrdimensionalen Lage- oder Konfigurationsraum dargestellt werden. Die vom System wirklich durchlaufene Bahnkurve wird mit benachbarten variierten Bahnkurven verglichen, die ebenfalls mit den Bindungen des Systems verträglich sind (Variation der Bahn). Befindet sich der i-te Massepunkt auf der wirklichen Bahn zum Zeitpunkt t am Ort r_i, so würde er sich auf der variierten Bahn um dr_i verschieben, d.h. am Ort r_i + dr_i befinden (Abb.); Anfangs- und Endpunkt der Bahn werden dabei nicht variiert, d.h., dr_i(t₀) = dr_i(t₁) = 0, wenn t₀ bzw. t₁ die zugehörigen Zeiten sind. Längs aller möglichen Bahnen wird die Lagrange-Funktion  bestimmt, die sich aus der kinetischen Energie T und der potentiellen Energie U des Systems zusammensetzt. Das Integral  ist eine Funktion (genauer: ein Funktional) der Bahnkurve im Lageraum; S heisst Wirkungsfunktion oder -integral, da es die Dimension einer Wirkung (d.i. Energie · Zeit) hat, oder auch Hamiltonsche Prinzipalfunktion (Wirkung). Das Hamiltonsche Prinzip besagt, dass die Wirkungsfunktion S für die wirklich durchlaufene Bahnkurve minimal (genauer: extremal) ist, d.h., dass die erste Variation dS von S für die wirkliche Bewegung verschwindet: . Greifen an dem vorliegenden System auch Kräfte ohne Potential U an, so muss das Hamiltonsche Prinzip in der allgemeinen Form  formuliert werden, wobei A die von diesen Kräften am System verrichtete Arbeit ist.

Das Hamiltonsche Prinzip kann auch mit beliebigen verallgemeinerten Koordinaten q_j und Geschwindigkeiten  zur Beschreibung eines Systems herangezogen werden. Bei holonomen Bindungen sind die verallgemeinerten Koordinaten q_j voneinander unabhängig; sie können daher auch unabhängig voneinander variiert werden. Aus dem Hamiltonschen Prinzip folgen dann die Lagrangeschen Gleichungen zweiter Art:

 bzw. .

Dabei muss die virtuelle Arbeit der eingeprägten Kräfte, 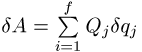 in Abhängigkeit von den verallgemeinerten Kräften (verallgemeinerte Koordinaten) ausgedrückt werden. Beim Vorliegen nichtholonomer Bindungen unterliegen die dq_j zusätzlichen Einschränkungen der Art 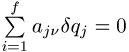 (n = 1, ..., k), wobei k die Anzahl nichtholonomer Bindungen ist, die mittels der Lagrangeschen Multiplikatorenmethode zu berücksichtigen sind. Die obigen Bewegungsgleichungen sind dann durch die Ausdrücke 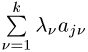 auf den rechten Seiten zu ergänzen: l_n sind insgesamt k unbestimmte Parameter (Lagrangesche Multiptikatoren), die zusammen mit den q_j aus den f Bewegungsgleichungen und den k Bindungsgleichungen zu bestimmen sind. Wegen der Äquivalenz der Lagrangeschen Gleichungen zweiter Art mit dem Hamiltonschen Prinzip wird bei praktischen Untersuchungen gewöhnlich von diesen ausgegangen, dies trifft besonders für nicht-mechanische Systeme zu (Feldtheorie).

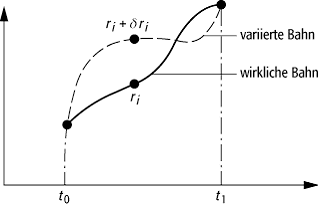
Hamiltonsches Prinzip: Wirkliche und variierte Bahn eines Massepunktes. Befindet sich der Massepunkt auf der wirklichen Bahn zum Zeitpunkt t am Ort r_i, so würde er sich auf der variierten Bahn um dr_i verschieben, d.h. am Ort r_i + dr_i befinden.