Techniklexikon

Diffusion

Wanderung eines Stoffes in Gasen, Flüssigkeiten oder Festkörpern aufgrund eines Konzentrationsgefälles. In der Elektronik: Gerichtete Bewegung von Teilchen aufgrund eines örtlichen Konzentrationsunterschieds, die zur Dotierung von Halbleitern genutzt wird. Meist versteht man unter D. auch die Diffusionsverfahren. Die Halbleitertechnik nutzt die D., um durch Erzeugen einer hohen Konzentration von Teilchen (Atome von r Dotanten) an der Oberfläche des Wa-fers diese in den Halbleiter einzubringen (Dotierung). Bei Temperaturen um 1000°C erhalten die Atome die dafür notwendige Beweglichkeit. Der Diffusionskoeffizient ist ein Maß für die Geschwindigkeit, mit der sich die Fremdatome im Halbleiter ausbreiten. Die maximale Konzentration, die dabei im Halbleiter erreicht werden kann, wird durch dessen Aufnahmevermögen für das entsprechende chemische Element bei der Diffusionstemperatur, die thermische Löslichkeit, bestimmt. Bei jeder weiteren Temperaturbehandlung durch Diffusions- oder Oxydationsschritte verändert sich die Verteilung der Dotanten im Halbleiter, das Diffusionspröfil. Die Gesamtheit aller Dotierungs-und Temperaturschritte muß so abgestimmt werden, daß das für die Funktion des Bauelements erforderliche Dotierungsprofil entsteht. Entsprechend den an der Oberfläche des Halbleiters herrschenden Bedingungen (Oxidschicht, Atmosphäre) unterscheidet man verschiedene D. verfahren. Meist ist eine D. durch eine Maske (Diffusionsfenster) erforderlich. Obwohl das Einbringen der Dotanten in den Halbleiter zunehmend durch Ionenimplantation erfolgt, bleibt die Bedeutung der D. für die Umverteilung der Dotanten bei Temperaturbehandlung erhalten. In der Fotografietechnik: Der Begriff wird vorwiegend in physikalischem Sinne gebraucht. Man versteht darunter das Bestreben nicht ortsgebundener, also freibeweglicher Teilchen (z. B. in Flüssigkeiten und Gasen), dank ihrer kinetischen Energie (Wärmebewegung) einen möglichst großen Raum einzunehmen, d. h. von einem Ort höherer Konzentration zu einem Ort niedrigerer Konzentration zu gelangen (Konzentrationsausgleich). Die Diffusionsgeschwindigkeit ist u. a. von der Teilchengröße (Molekülgröße) und Temperatur abhängig. So kann z. B. das Herausdiffundieren wasserlöslicher Farbkuppler aus der Farbfilmemulsion während der Entwicklung nur dadurch vermieden werden, daß die relativ kleinen Moleküle an organische Verbindungen mit ausreichender Teilchengröße gekuppelt werden, welche sich ihrerseits nicht aus der Filmschicht herauslösen lassen. Auch der Kanteneffekt ist auf Diffusion von Entwickler einerseits und von entwicklungshemmenden Substanzen andererseits während der Filmentwicklung zurückzuführen. Im optischen Bereich wird der Begriff Diffusion meist im Zusammenhang mit der Streuung des Lichts durch Beugung, Brechung (Lichtbrechung) oder Reflexion benutzt. Thermodynamik und statistische Physik, Konzentrationsausgleich durch molekularen Massentransport zwischen verschiedenen Teilvolumina eines makroskopischen Systems nach einer Zusammensetzungsänderung. Ein Beispiel ist die sich im Laufe der Zeit vollständig einstellende Durchmischung zweier verschiedener, zu einem ursprünglichen Zeitpunkt getrennter Gase oder Flüssigkeiten. Die treibende Kraft dieser stets irreversiblen, also unter Zunahme der Gesamtentropie ablaufenden Diffusionsprozesse ist die thermische Agitation der Moleküle (Brownsche Bewegung). Die Diffusion in Gasen - ein bekanntes Beispiel ist die Ausbreitung von Duftstoffen in der Luft - verläuft aufgrund der geringeren Dichte und der stärkeren thermischen Bewegung meist schneller als die in Flüssigkeiten, in denen die Durchmischung zweier Phasen bei Abwesenheit von Strömungsbewegungen bisweilen Monate dauern kann. In Festkörpern, in denen die Bewegungsmechanismen anderer Art sind, finden solche Prozesse in nochmals deutlich längeren Zeitskalen statt. In jedem Falle ist eine starke Temperaturabhängigkeit zu beobachten; je höher die Temperatur ist, desto schneller laufen diffusive Prozesse ab, und am absoluten Temperaturnullpunkt, an dem jede thermische Bewegung zum Erliegen kommt, sollte auch keine Diffusion mehr stattfinden. Man unterscheidet zwischen

1) Fremd- oder Gegendiffusion, der durch ein Konzentrationsgefälle verursachten Bewegung von Fremdteilchen in einem anderen Stoff;

2) Selbst- oder Eigendiffusion, der von einem Dichtegradienten hervorgerufenen Bewegung von Partikeln in einer gleichartigen Umgebung;

3) von einem Temperaturgradienten im System herrührender Thermodiffusion, die in Gasen und Flüssigkeiten eine nur unwesentliche Rolle spielt (dazu siehe unten);

4) der von einem Druckgradienten verursachten Druckdiffusion; und

5) Rotationsdiffusion, der Orientierungsänderung nicht-kugelsymmetrischer Partikel in flüssigen Systemen, die stets in Richtung einer völlig regellosen Orientierung der Symmetrieachsen verläuft. Dieser Mechanismus verhindert z.B die völlige Ausrichtung polarer Moleküle in einem elektrischen Feld.

Die mathematische Behandlung isothermer Diffusionsprozesse in räumlich isotropen Systemen basiert auf den beiden Fickschen Gesetzen, die der deutsche Physiologe A. Fick 1855 formulierte. Die erste dieser beiden Gesetzmässigkeiten beschreibt den durch einen Konzentrationsgradienten dc/dx verursachten Durchtritt von N Molekülen durch eine Querschnittsfläche A je Zeitintervall:

 .

Der Proportionalitätsfaktor D, der als Diffusionskoeffizient oder Diffusionskonstante bezeichnet wird, ist ein Mass für die Häufigkeit der Zusammenstösse der Partikel, also zur mittleren freien Weglänge und zur mittleren Geschwindigkeit der Moleküle proportional, und seine Dimension ist cm² s ^{- 1}. In der Diffusionskonstanten ist die gesamte Temperaturabhängigkeit des Prozesses parametrisiert; näheres dazu siehe unten. Ausgehend von dieser ersten Gleichung gelangt man zu einer zeitabhängigen Beschreibung in Form des zweiten Fickschen Gesetzes durch Berücksichtigung der Kontinuitätsgleichung für die Teilchenzahlerhaltung:

 .

Diese Beziehung wird auch einfach als Ficksches Gesetz oder Diffusionsgleichung, ein dieser Gesetzmässigkeit gehorchender Vorgang als Ficksche Diffusion bezeichnet.

Tatsächlich gelten die phänomenologisch motivierten Fickschen Gesetze nur im Grenzfall geringer Konzentrationen; eine strengere theoretische Betrachtung im Rahmen der makroskopischen irreversiblen Thermodynamik berücksichtigt neben dem Einfluss eines Temperatur- und eines Druckgradienten auch äussere Kräfte. Die Stromdichte des sogenannten Diffusionstroms j, der infolge der Relativbewegungen der Partikel auftritt, kann als

mit zwei Parametern a und b angesetzt werden, wenn die Gradienten des chemischen Potentials m, des Potentials der äusseren Kraft V und der Temperatur T nicht zu gross sind. Der Vergleich mit den fundamentalen phänomenologischen Gleichungen der irreversiblen Thermodynamik

,

die über die kinetischen Koeffizienten g_ij den Zusammenhang der Änderung der makroskopischen Parameter X_i mit der Änderung der Entropie S herstellen, zeigt, dass  und  gelten muss, so dass die Diffusionsstromdichte als

geschrieben werden kann. Der letzte Term der rechten Seite dieser wichtigen Gleichung beschreibt die besonders bei der Behandlung der metallischen Leitfähigkeit wichtige Thermodiffusion, die in Gasen und Flüssigkeiten keine entscheidende Rolle spielt. Geht man vom chemischen Potential m zu den Variablen c, T und dem Druck p über, so erhält man den allgemeinsten Auduck für den Diffusionsstrom

mit dem Barodiffusionskoeffizienten D_p, der die Druckdiffusion beschreibt, dem Thermodiffusionskoeffizienten D_T und der Beweglichkeit B. Die Stromdichte zerfällt also in den durch das Konzentrationsgefälle verursachten, den durch den Druck- und den durch den Temperaturgradienten hervorgerufenen Anteil der Diffusion und einen von der äusseren Kraft  abhängigen Driftanteil (Driftbewegung).

Die allgemeine Diffusionsgleichung in Form einer Differentialgleichung für die Konzentration ergibt sich, indem man mit Hilfe der Kontinuitätsgleichung  die Stromdichte eliminiert; beschränkt man sich auf isotherme und isobare Vorgänge, so vereinfacht sie sich zur inhomogenen Diffusionsgleichung

,

die für V = const. wieder in das Ficksche Gesetz übergeht. Dabei ist  die mittlere Teilchenkonzentration, D wieder die Diffusionskonstante und B die Beweglichkeit gegenüber äusseren Kräften. Diese letzten beiden Koeffizienten, die im übergeordneten Konzept der Transporttheorie als Transportkoeffizienten verstanden werden können, berechnen sich gemäss:

.

Für ideale Gase ist der Selbstdiffusionskoeffizient , mit der mittleren thermischen Geschwindigkeit v und der mittleren freien Weglänge l. Für zwei Gase mit den Molmassen m₁ und m₂, dem mittleren Stossquerschnitt s₁₂ und den Dichten n₁ und n₂ liefert die kinetische Gastheorie:

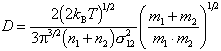
Die Diffusionskonstante ist also umgekehrt propotional zur Wurzel aus dem Molekulargewicht. Im Rahmen der Einsteinschen Theorie der Brownschen Bewegung gelangt man unter der Voraussetzung, dass der Moleküldurchmesser a gross gegenüber der mittleren freien Weglänge ist, zu den Ausdrücken

für die translatorische Diffusionskonstante D und die Rotationsdiffusionskonstante D_rot. R ist hier die Gaskonstante, h die Viskosität der Umgebung.

Wichtige Anwendungen findet die Diffusion bei der Trennung von Gasen verschiedener molarer Masse, insbesondere von verschiedenen Isotopen des gleichen chemischen Elements - das bekannteste Beispiel hierfür ist die Trennung der beiden Wasserstoffisotope mit den relativen Atommassen 1 und 2 durch G. Hertz im Jahr 1932 -, in der von Gaede 1915 entwickelten Diffusionspumpe, mit deren Hilfe man Vakua bis zu 10 ^{- 9} Pa erreichen kann, und in der Halbleitertechnik, in der Diffusionsprozesse u.a. für gezielte Dotierungen von Halbleiterkristallen eingesetzt werden. [JS2]

Diffusion: Grössenordnung der Diffusionskonstanten.

bottom:solid black 1.1pt;mso-border-top-alt:.75pt;mso-border-left-alt: .6pt;mso-border-bottom-alt:1.1pt;mso-border-right-alt:.6pt;mso-border-color-alt: black;mso-border-style-alt:solid;padding:0cm 0cm 0cm 0cm\'> Aggregatzustand	bottom:solid black 1.1pt;border-right:solid black 1.0pt; mso-border-left-alt:solid black .6pt;mso-border-top-alt:.75pt;mso-border-left-alt: .6pt;mso-border-bottom-alt:1.1pt;mso-border-right-alt:.6pt;mso-border-color-alt: black;mso-border-style-alt:solid;padding:0cm 0cm 0cm 0cm\'> D [cm2/s]
Gase	10 - 1-1
Flüssigkeiten	10 - 5
bottom:solid black 1.0pt;border-right:none; mso-border-left-alt:solid black .75pt;mso-border-bottom-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'> Festkörper	bottom:solid black 1.0pt;border-right:solid black 1.0pt;mso-border-bottom-alt: solid black .75pt;mso-border-right-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'> 10 - 5-10 - 20

 

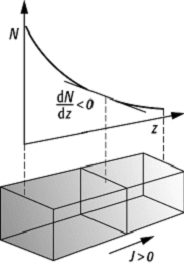
Diffusion: Zur Illustration des Fickschen Gesetzes.