Techniklexikon

komplexe Dielektrizitätskonstante

Elektrodynamik und Elektrotechnik, e^*, verallgemeinerte, frequenzabhängige Dielektrizitätskonstante. Der einfache Ansatz D = eE (D: dielektrische Verschiebung, E: elektrische Feldstärke) für die Dielektrizitätskonstante e  = e_r / e₀ (e₀, e_r: Dielektrizitätskonstante im Vakuum bzw. im betrachteten Medium) gilt für zeitlich veränderliche Felder nur noch für einzelne Frequenzkomponenten in der Fourier-Entwicklung: D(w) = e(w)E(w). Für eine ebene Welle E(x,t) = e^i(k×x-wt) im nichtleitenden Dielektrikum folgt dann aus der vierten Maxwell-Gleichung, verallgemeinert auf leitende Medien:

rotH = ¶D / ¶t + j = -e(w) ¶E / ¶t + s(w)E (1),k´H = -w (w) +is(w) / w) E =: -e^*(w) E (2),

mit e^*(w) = e(w) + is(w) / w (3)

als allgemeiner, frequenzabhängiger und komplexer Dielektrizitätskonstanten in beliebigen (isotropen) Medien (H: magnetische Feldstärke, s(w): elektrische Leitfähigkeit, j: Stromdichte). Der Phasenwinkel von e^*(w), d(w), mit tand(w) = Ime^*(w) / Ree^*(w) = w e(w) / s(w) heisst auch Verlustwinkel und beschreibt eine Phasenverschiebung zwischen E(w) und D(w), die zu dielektrischen Verlusten führt. Diese Phasenverschiebung beruht anschaulich auf dem "Nachhinken" der Reaktion der atomaren Dipole auf die erregende elektrische Welle (elektrische Polarisation).

Die Frequenzabhängigkeit von e^*(w) wird durch die atomare Theorie der Dispersion erklärt; e^*(w) ist mit der komplexen Brechzahl n^* über die Maxwell-Relation n* =  verknüpft. Mit der Drudeschen Formel gilt näherungsweise: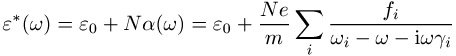(a(w): komplexe Polarisierbarkeit, N, m: Dichte und Masse der atomaren Resonatoren, f_i, w_i, g_i: Oszillatorstärke, Resonanzfrequenz und Dämpfungskonstante der verschiedenen Resonanzen). Für freie Elektronen im Leiter kann e^*(w) in einen Isolator-Anteil e(w) und einen Leiter-Anteil aufgetrennt werden:

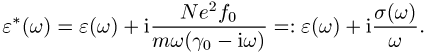
Durch Vergleich mit (3) ergibt sich also s(w) = f₀Ne² / m(g₀-iw) = s₀ / m(1-iwt), dabei ist f₀N die Dichte der Leitungselektronen, s₀ die Gleichstromleitfähigkeit und t = 1 / g₀ = m_es₀ / Ne² die Relaxationszeit der durch das äussere Feld angeregten Schwingungen der Leitungselektronen. Im Bereich der Resonanzfrequenzen w_i nimmt Ree^*(w) = e(w) stark ab und Ime^*(w) wird maximal (anormale Dispersion). In den übrigen Frequenzbereichen ist Ime^*(w) » 0, e^*(w) ist also reell und wächst langsam mit der Frequenz (normale Dispersion). Wichtige Resonanzen sind die Orientierungspolarisation permanenter Dipole bei ca. 10¹⁰ Hz. Der Beitrag der Orientierungspolarisation zu e^*(w) kann auch mit den Debye-Gleichungen beschrieben werden. Im infraroten Spektralbereich liegen die Schwingungen der Ionen im Kristallgitter und im optischen und ultravioletten Bereich die Verschiebungspolarisation der gebundenen Elektronen. Im Hochfrequenzlimes (harte Röntgenstrahlen und darüber) wird e^*(w) wieder reell und es gilt e(w) » 1-w_Pl^² / w^² < 1 (w_Pl: Plasmafrequenz). Bei diesen Frequenzen sind auch Metalle "durchsichtig". Diese Formel gilt auch für ein ideales, stossfreies Plasma, mit Stössen wird e(w) wiederum komplex.

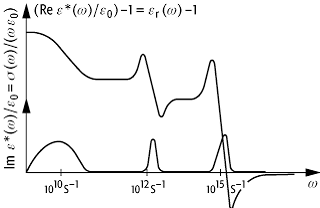
komplexe Dielektrizitätskonstante: Schematische Darstellung der Frequenzabhängigkeit der komplexen Dielektrizitätskonstanten e^*(w).