Brechzahl

Irene Kramer-Schwenk
Brechungsindex, Kurzzeichen n, Kennzahl eines optischen Materials. Die Brechzahl ist ein Mass für die Fortpflanzungsgeschwindigkeit c1 des Lichtes im betrachteten Medium M1. Die auf die Vakuumlichtgeschwindigkeit c bezogene Geschwindigkeit in einem Medium M1 nennt man absolute Brechzahl, die auf die Lichtgeschwindigkeit in einem zweiten Medium M2 bezogene Ausbreitungsgeschwindigkeit heisst relative Brechzahl n12; letztere bestimmt nach dem Snelliusschen Brechungsgesetz sin a / sin b = c1/c2 = n2/n1 = n12 den Winkel, mit dem ein Lichtstrahl, d.h. eine ebene elektromagnetische Welle, an der Grenzfläche der beiden Medien gebrochen wird.
Die absolute Brechzahl für feste und flüssige Materialien liegt i.a. zwischen 1 und 2 (Tabelle). Ist n1 > n2, so ist das Material mit n1 optisch dichter und dasjenige mit n2 optisch dünner.
Brechzahl: Absolute Brechzahlen verschiedener Materialien bei einer Temperatur von 20 °C und einer Wellenlänge von 589 nm.
|
Material |
Brechzahl |
|
Vakuum |
1 |
|
Flintglas |
1,613 |
|
Kronglas |
1,510 |
|
Wasser |
1,333 |
|
Luft (1013 mbar) |
1,000272 |
|
Diamant |
2,417 |
Diese elementare Definition der Brechzahl als Quotient zweier
Ausbreitungsgeschwindigkeiten hat nur im Spezialfall der geometrischen Optik
Optik, bei der kleine Wellenlängen in transparenten Medien betrachtet werden,
Gültigkeit. Für die allgemeine Definition der Brechzahl betrachtet man eine
ebene monochromatische Welle, deren Ausbreitung durch den Faktor ![]() bestimmt wird. Für den Betrag der im
allgemeinen komplexen Wellenzahl k gilt der Zusammenhang
bestimmt wird. Für den Betrag der im
allgemeinen komplexen Wellenzahl k gilt der Zusammenhang ![]() mit der Permeabilitätszahl mr, der
Dielektrizitätszahl er und der Vakuumlichtgeschwindigkeit c. Diese
Gleichung kann als die Definition für die Brechzahl n und die
Dämpfungskonstante bzw. den Absorptionskoeffizienten c verstanden werden.
Diese Koeffizienten können zu einer komplexen verallgemeinerten Brechzahl
mit der Permeabilitätszahl mr, der
Dielektrizitätszahl er und der Vakuumlichtgeschwindigkeit c. Diese
Gleichung kann als die Definition für die Brechzahl n und die
Dämpfungskonstante bzw. den Absorptionskoeffizienten c verstanden werden.
Diese Koeffizienten können zu einer komplexen verallgemeinerten Brechzahl ![]() zusammengefasst werden. Da die komplexen
Parameter mr und insbesondere er im allgemeinen stark
von der Frequenz w der eingestrahlten Welle abhängen, ist auch die
verallgemeinerte Brechzahl ñ eine von der Frequenz
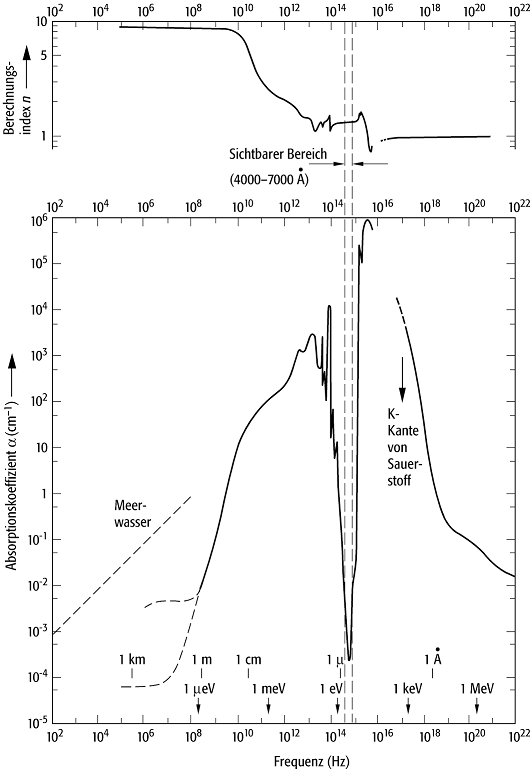
abhängige Funktion (Abb.). Der oben angegebene Exponentialfaktor der
Wellenausbreitung kann dann als
zusammengefasst werden. Da die komplexen
Parameter mr und insbesondere er im allgemeinen stark
von der Frequenz w der eingestrahlten Welle abhängen, ist auch die
verallgemeinerte Brechzahl ñ eine von der Frequenz
abhängige Funktion (Abb.). Der oben angegebene Exponentialfaktor der
Wellenausbreitung kann dann als ![]() geschrieben werden; der Realteil der Brechzahl
n ist also, in Übereinstimmung mit der elementaren Definition aus der
geometrischen Optik, die auf c bezogene Ausbreitungsgeschwindigkeit der
Welle, während die Dämpfungskonstante c die exponentielle
Dämpfung der Welle während ihrer Fortpflanzung im Medium beschreibt. Es sei
darauf hingewiesen, dass diese Dämpfung nicht unbedingt mit einer echten
Absorption verbunden sein muss. Dissipation der Energie, also Absorption, tritt
nur auf, wenn er
und mr einen von null
verschiedenen Imaginärteil aufweisen (komplexe Dielektrizitätskonstante),
während der Koeffizient c auch bei reellen (negativen) er und mr von null verschieden
sein kann (z.B. bei Streuverlusten der Strahlung innerhalb des Materials). Die
Frequenzabhängigkeit der Permeabilität ist nur schwach ausgeprägt; für die
meisten Stoffe ist sogar mr » 1, so dass gilt
geschrieben werden; der Realteil der Brechzahl
n ist also, in Übereinstimmung mit der elementaren Definition aus der
geometrischen Optik, die auf c bezogene Ausbreitungsgeschwindigkeit der
Welle, während die Dämpfungskonstante c die exponentielle
Dämpfung der Welle während ihrer Fortpflanzung im Medium beschreibt. Es sei
darauf hingewiesen, dass diese Dämpfung nicht unbedingt mit einer echten
Absorption verbunden sein muss. Dissipation der Energie, also Absorption, tritt
nur auf, wenn er
und mr einen von null
verschiedenen Imaginärteil aufweisen (komplexe Dielektrizitätskonstante),
während der Koeffizient c auch bei reellen (negativen) er und mr von null verschieden
sein kann (z.B. bei Streuverlusten der Strahlung innerhalb des Materials). Die
Frequenzabhängigkeit der Permeabilität ist nur schwach ausgeprägt; für die
meisten Stoffe ist sogar mr » 1, so dass gilt ![]() .
.
Für echte Dielektrika tritt ausserhalb der Resonanzstellen von er(w), an denen das Medium
optisch transparent ist, keine wesentliche Absorption auf; er ist dort also reell,
und es gilt die sog. Maxwell-Relation ![]() . Es ist
. Es ist ![]() und damit auch dn/dw >
0. Dieses Verhalten wird als normale Dispersion bezeichnet; bei einer
Abweichung von dieser Monotonie liegt anomale Dispersion vor (Dispersion). Für
grosse Absorptionskoeffizienten kann n kleiner als eins werden (z.B. bei
Röntgenstrahlen in Glas).
und damit auch dn/dw >
0. Dieses Verhalten wird als normale Dispersion bezeichnet; bei einer
Abweichung von dieser Monotonie liegt anomale Dispersion vor (Dispersion). Für
grosse Absorptionskoeffizienten kann n kleiner als eins werden (z.B. bei
Röntgenstrahlen in Glas).
Für metallische Leiter ist der Imaginärteil der
Dielektrizitätszahl ![]() (mit der elektrischen Leitfähigkeit s)
gross gegenüber dem Realteil; Brechzahl und Dämpfungskonstante sind dann
näherungsweise gleich:
(mit der elektrischen Leitfähigkeit s)
gross gegenüber dem Realteil; Brechzahl und Dämpfungskonstante sind dann
näherungsweise gleich: ![]() . Die
Leitfähigkeit bestimmt also die Eindringtiefe der elektromagnetischen Wellen in
das Metall.
. Die
Leitfähigkeit bestimmt also die Eindringtiefe der elektromagnetischen Wellen in
das Metall.
Die Reflexion elektromagnetischer Wellen an Grenzflächen zwischen zwei Medien wird ebenfalls durch die Brechzahl bestimmt; für optisch transparente Medien gilt, wie bereits erwähnt, das Snelliussche Brechungsgesetz, und für die Reflexion einer elektromagnetischen Welle, die senkrecht aus dem Vakuum auf ein Medium mit der verallgemeinerten Brechzahl ñ = n + i c fällt, ergibt sich das Reflexionsvermögen R zu
![]()
Durch Temperaturänderungen, elektrische und magnetische Felder sowie hohe Strahlungsintensitäten (nichtlineare Optik) kann die Brechzahl geringfügig beeinflusst werden.
Brechzahl: Realteil (oben) und Imaginärteil (Dämpfungskonstante, unten) der verallgemeinerten Brechzahl von flüssigem Wasser als Funktion der Frequenz. Der sichtbare Bereich normaler Dispersion, in dem die Dämpfung sehr gering wird, ist markiert.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.