Techniklexikon

Resonatoren

Laserphysik und -technik, all jene Systeme, die die Aufrechterhaltung einer Schwingung (typischerweise elektromagnetischer, elektrischer oder akustischer Natur) erlauben. Neben den elektrischen Resonatoren sind die optischen Resonatoren in der Physik und Technik am verbreitetsten. Die grösste Bedeutung kommt hier den Spiegelresonatoren zu, die eines der wichtigsten Werkzeuge der Laserphysik sind (Laser, Laserresonator); es existieren aber auch Wellenleiter-Resonatoren und DFB-Systeme. Zur Berechnung des Einflusses von Beugungseffekten muss die skalare Beugungstheorie verwendet werden; die meisten Spiegelresonatoren lassen sich jedoch gut durch die geometrische Optik beschreiben. In der paraxialen Näherung beschränkt man sich hierbei auf achsennahe Strahlen im Resonator. Dies erlaubt die Darstellung des Resonators und weiterer optischer Elemente durch zweidimensionale Matrizen (Matrixoptik).

Einer der wichtigsten Aspekte eines Resonators ist die Frage nach seiner optischen Stabilität. In einer stabilen Konfiguration wird ein Strahl auch nach vielen Umläufen den Resonator nicht verlassen. Mit den Stabilitätsparametern , abhängig vom Spiegelabstand d und den Krümmungsradien R_i, lässt sich das Stabilitätskriterium  herleiten. Anschaulich bedeutet dies, dass die beiden Strahlen von den Krümmungsmittelpunkten der Spiegel zur jeweiligen Spiegelfläche teilweise überlappen müssen (siehe Abb. 1). Anhand der obigen Ungleichung kann man ein allgemeines Stabilitätsdiagramm erstellen (siehe Abb. 2).

Man unterscheidet geschlossene Resonatoren, wie z.B. Hohlleiter, und offene Resonatoren, die die elektromagnetische Welle meist nur in einer Raumrichtung eingrenzen und für den optischen Einsatz typisch sind. Optische Resonatoren sind typischerweise offen und bestehen aus zwei oder mehreren Spiegeln oder entsprechenden reflektierenden Elementen, wie etwa optischen Gittern. Die wichtigsten Typen der stabilen optischen Resonatoren werden nach Krümmungsradius und Spiegelabstand charakterisiert. Gilt R₁ = R₂, dann spricht man (bei beliebigem d) von einem symmetrischen Resonator. Der ebene oder planare Resonator, mit R₁ = R₂ = ¥, besteht aus zwei planparallelen Spiegeln in beliebigem Abstand (Fabry-Pérot-Resonator). Desweiteren unterscheidet man fokale, konfokale und konzentrische (sphärische) Typen (siehe Tab. und Abb. 2+3). Betrachtet man die sich ausbreitenden Wellenfronten eines konfokalen Resonators, dann erhält man einen äquivalenten Resonator, indem man am Ort einer Wellenfront einen Spiegel mit gleichem Krümmungsradius plaziert. Der semi-konfokale Resonator ist demnach äquivalent zum konfokalen Resonator, bei dem am Ort der ebenen Wellenfront in der Mitte ein planarer Spiegel eingesetzt wurde (siehe Abb. Strahltaille).

Desweiteren charakterisiert man Resonatoren entsprechend ihrer Geometrie nach linearen, gefalteten und ringförmigen Typen. Im linearen Resonator pflanzt sich die Strahlung in beiden Richtungen entlang einer einzigen optische Achse fort, wie z.B. bei den oben erwähnten stabilen optischen Resonatoren, so dass sich eine stehende Welle ausbildet. Der gefaltete Resonator besteht im Prinzip aus zwei oder mehreren kombinierten linearen Resonatoren, die in einem Winkel zueinander angeordnet sind, z.B. V-förmig bei zwei, oder Z-förmig bei drei Armen. Gefaltete Resonatoren werden eingesetzt, um z.B. wellenlängenselektierende Elemente wie holographische Gitter in den Resonator zu integrieren oder um das gesamte Resonatorsystem kompakter zu gestalten. Im Ringresonator kann sich entweder eine stehende Welle ausbilden oder - beim Einsatz einer optischen Diode - eine fortlaufende Welle, so dass sich die Strahlung im Resonator nur in einer Richtung ausbreitet.

Die spektralen Eigenschaften eines Resonators werden durch verschiedene Parameter beschrieben. Wichtigster Gesichtspunkt ist meist die Resonanzfrequenz n_R, bei der sich, entsprechend der Resonanzbedingung, eine stehende Welle ausbilden kann. Sie ergibt sich aus der optischen Länge, l, des Resonators zu , mit .

Die Resonatorgüte (Q-Wert) ist ein Mass für die Dämpfung der Schwingung während eines Umlaufs. Hohe Q-Werte bedeuten, dass ein Photon im Durchschnitt viele Male im Resonator umläuft, bevor es absorbiert wird oder den Resonator verlässt; sie sind besonders in der Verstärkung schwächster Signale von Bedeutung (z.B. beim Ein-Atom-Maser). Die Resonatorgüte ist nicht nur von Absorptions- und Transmissions- und Streuungsverlusten abhängig, sondern auch von Beugungseffekten. Ein Mass der Beugungseinflüsse für eine bestimmte Wellenlänge l gibt die Fresnel-Zahl,  (a: maximal möglicher Strahlradius, bestimmt durch optische Elemente wie z.B. Blenden usw.). Resonatoren mit grosser Fresnel-Zahl besitzen entsprechend kleine Beugungsverluste. Von der Güte abhängig ist die Resonanzbreite, die angeben, in welchem Frequenzintervall dn der Resonator eine Schwingung ohne wesentliche Dämpfung aufrecht erhalten kann. Typischerweise werden die möglichen Resonanzfrequenzen und auch deren jeweilige Resonanzbreiten durch wellenlängenselektierende Elemente im Resonator begrenzt.

Resonatoren: Stabile optische Resonatortypen, R_i: Spiegelradien, d: Spiegelabstand, g_i: Stabilitätsparameter.

Typ	bottom:solid black 1.0pt;border-right:none; padding:0cm 3.55pt 0cm 3.55pt\'> Spiegelradien	Stabilitätsparameter
symmetrisch	R1 = R2	g1 = g2
eben (planar)	R1 = R2 = ¥	g1 = g2 = +1
fokal, symmetrisch	R1 = R2 = 2d	g1 = g2 = 1 / 2
konfokal, symmetrisch	R1 = R2 = d	g1 = g2 = 0
konfokal, allgemein	R1 + R2 = 2d	g1 + g2 = 2 g1 g2
semi-konfokal	R1 = 2d, R2 = ¥	g1 = 1 / 2, g2 = 1
konzentrisch (sphärisch), symmetrisch	R1 = R2 = d / 2	g1 = g2 = -1
bottom:solid black 1.0pt;border-right:none; padding:0cm 3.55pt 0cm 3.55pt\'> konzentrisch, allgemein	bottom:solid black 1.0pt; padding:0cm 3.55pt 0cm 3.55pt\'> R1 + R2 = d	bottom:solid black 1.0pt;border-right:solid black 1.0pt; padding:0cm 3.55pt 0cm 3.55pt\'> g1g2 = 1

 

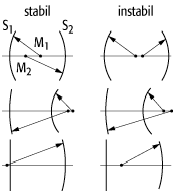
Resonatoren 1: Stabilitätsfaustregeln für Resonatoren. Die Strecken vom Krümmungsmittelpunkt, M_i, der beiden Spiegel zur jeweiligen Spiegelfläche, S_i, müssen teilweise überlappen, damit der Resonator stabil ist. (Eine Strecke darf weder komplett ausserhalb noch komplett innerhalb der anderen liegen.)

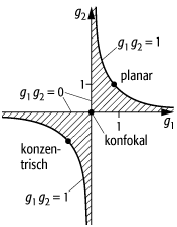
Resonatoren 2: Stabilitätsdiagramm optischer Spiegelresonatoren. In den schraffierten Bereichen ist das Stabilitätskriterium erfüllt und der Resonator stabil. Einige typische Resonatorentypen sind eingetragen (g_i: Stabilitätsparameter).

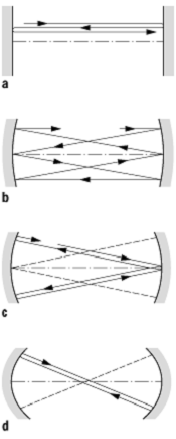
Resonatoren 3: Die wichtigsten stabilen optischen Resonatorentypen: a) planar (Fabry-Pérot), , ; b) fokal, symmetrisch, , ; c) konfokal, symmetrisch, , ; d) spärisch (konzentrisch), symmetrisch, , .