Kommutator

Kollektor QuantenmechanikMathematische Methoden und Computereinsatz, 1) Elektrotechnik: Stromwender, Elektromotor.

2) Mathematik: Operator, der aus der Vertauschung des Produktes zweier Operatoren P₁ und P₂ hervorgeht. Der Kommutator ist definiert als

Als Beispiel aus der Quantenmechanik seien der Orts- und Impulsoperator und deren Vertauschungsrelation genannt. Aus der Definition des Kommutators lassen sich eine Vielzahl nützlicher Identitäten ableiten:

sowie die Jacobi-Identität. Schliesslich gilt das Distributivgesetz

In der klassischen Mechanik sind für zwei beliebige skalare Funktionen f und g der Koordinaten q und Impulse p sind die Poissonschen Klammern

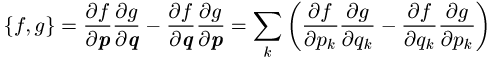
als spezieller Kommutator definiert. Für sie gelten ebenfalls die obigen Kommutatorbeziehungen.

Schliesslich lässt sich neben dem Kommutator für zwei Operatoren P₁ und P₂ der Antikommutator

definieren.

3) Quantenmechanik: Bezeichnung für die Differenz AB - BA der Produkte AB und BA zweier im allgemeinen nicht vertauschbaren Grössen (d.h. AB ¹ BA) in der Quantentheorie, wie sie z.B. eine Matrix oder ein Differentialoperator darstellen. Diese Abbildung wird abgekürzt mit der Schreibweise [A,B] und die Kommutatorrelation lautet dann: [A,B] = AB - BA. In der Wellenmechanik werden der Teilchenort durch den Operator x und der Teilchenimpuls durch den Operator  dargestellt. Der Kommutator der beiden Operatoren x und p, , charakterisiert das Problem der Reihenfolge der Operatoren im Operatorprodukt und zugleich den engen Zusammenhang der Quantenmechanik mit dem Planckschen Wirkungsquantum . Bekannte Beispiele nicht-kommutierender Matrizen sind die Dirac-Matrizen. Neben dem Kommutator kennt die Quantentheorie auch einen Antikommutator {A,B} = AB + BA. Bei ihm ist im Gegensatz zum Kommutator das Problem derReihenfolge der Operatoren im Operatorenprodukt irrelevant. Er spielt eine grosse Rolle in der Dirac-Theorie (Dirac-Gleichung).