Techniklexikon

Boltzmann-Gleichung

Boltzmannsche Stossgleichung, nichtlineare Integrodifferentialgleichung der statistischen Physik des Ungleichgewichts zur Beschreibung verdünnter Gase mit fast freier Bewegung der Moleküle. Diese 1872 von L. Boltzmann aufgestellte Grundgleichung der Kinetischen Gastheorie spielte in der Entwicklung der theoretischen Physik eine bedeutende Rolle und trug insbesondere dazu bei, die Vorstellung vom diskontinuierlichen, also atomaren Aufbau der Materie durchzusetzen (Atomismus). Ausgehend von dieser Gleichung entwickelte Boltzmann die allgemeine Transportgleichung und das H-Theorem.

Die Boltzmann-Gleichung beschreibt den Einfluss molekularer Zweierstösse auf die lokale Besetzungsdichte im Phasenraum eines Gases, das hinreichend verdünnt ist, um Stösse von mehr als zwei Partikeln vernachlässigbar zu machen. Zwischen den Stössen bewegen sich die N Moleküle des Gases frei, so dass der Phasenraum in die N sechsdimensionalen m-Räume
(r_i, u_i )_{i = 1...N} zerfällt. Es wird nun die Einteilchendichte f₁ im m-Raum eingeführt, so dass f₁(r, , t) d³r d³ die Anzahl der Moleküle mit dem Ort und der Geschwindigkeit im Intervall [r, r + dr] bzw. [,  + d] ist. Die elementare Ableitung der Boltzmann-Gleichung geht von Boltzmanns Annahme des molekularen Chaos, auch als Stosszahlansatz bezeichnet, aus; danach ist die Korrelation der Moleküle, die sich infolge eines Stosses ausbildet, bis zum nächsten Stoss wieder völlig verwischt, so dass die Gaspartikel statistisch unabhängig voneinander sind. Das Fehlen jeder Korrelation impliziert nun, dass die Dichte von Molekülpaaren im m-Raum die sogenannte Paarverteilungsfunktion f₂(r, , r₁, ₁, t), sich einfach als Produktansatz schreiben lässt:

.

Unter Voraussetzung dieses Stosszahlansatzes können die Molekülstösse in der gleichen Weise beschrieben werden wie etwa bei einem Molekularstrahlexperiment, was zur Boltzmann-Gleichung

führt. Dabei wurden die abkürzenden Schreibweisen  und  verwendet, wobei die gestrichenen Geschwindigkeiten diejenigen nach dem Stoss sind und  der totale Streuquerschnitt ist.

Eine alternative Herleitung der Boltzmann-Gleichung ergibt sich bei Betrachtung der BBGKY-Hierarchie.

Der Integralterm der rechten Seite, das sogenannte Stossintegral, beschreibt den Einfluss der Zweierstösse auf die Dynamik des Systems. Bei Fortlassen dieses Terms gelangt man zur kinetischen Gleichung für ein ideales Gas, die auch als stossfreie Boltzmann-Gleichung bezeichnet wird. Das als Konsequenz des Stosszahlansatzes auftretende Stossintegral, das die Nichtlinearität der Gleichung bewirkt, bedingt auch den Verlust der Zeitumkehrinvarianz, die den zugrunde liegenden mikroskopischen Zweierstössen noch zu eigen ist. Diese Auszeichnung einer bestimmten Zeitrichtung manifestiert sich im Boltzmannschen H-Theorem, dem zufolge die Zeit stets in Richtung der Abnahme oder, im Grenzfall, der Konstanz einer gemäss  zu berechnenden Funktion H(t) verläuft.

Es lässt sich zeigen, dass im Gleichgewichtsfall, also bei Konstanz von H, die Lösung für den Logarithmus der Verteilungsfunktion ln f eine Linearkombination von fünf möglichen sogenannten Stossvarianten a_i()_{i = 0...4} sein muss. Diese Stossvarianten sind

.

Als exakte Lösung für f ergibt sich die Maxwell-Verteilung

.

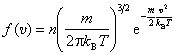Als Lösung für näherungsweise reversibel verlaufende Prozesse kann man eine Maxwell-Verteilung f(,r,t) mit lokal variierender Dichte, Temperatur und Strömungsgeschwindigkeit, die sogenannte lokale Gleichgewichtsverteilung, ansetzen. Dieser Ansatz für nicht zu grosse Abweichungen vom absoluten Gleichgewicht ist die Grundlage der hydrodynamischen Beschreibung eines Gases.

Die Boltzmann-Gleichung ist die Grundgleichung der Kinetischen Gastheorie. Sie gestattet die Berechnung der Verteilungsfunktion der Moleküle während des Ablaufs irreversibler Prozesse. Gleichzeitig kann die Boltzmann-Gleichung auch als grundlegend für die Transporttheorie betrachtet werden, da sich die fundamentale allgemeine Transportgleichung unmittelbar aus der Multiplikation mit einer beliebigen zeitabhängigen Grösse und anschliessender Integration über alle Geschwindigkeiten ergibt. Dies führt dann zur Berechnung der elektrodynamischen, thermodynamischen und hydrodynamischen Transportkoeffizienten, so z.B. des Diffusions- und des Thermodiffusionskoeffizienten sowie der Koeffizienten der elektrischen und der Wärmeleitfähigkeit. Einige der hauptsächlichen Anwendungsbereiche der Boltzmann-Gleichung sind:

1) Die hydrodynamischen Grundgleichungen ergeben sich als Grenzfall eines Quasigleichgewichts, also langsamer und schwacher zeitlicher und räumlicher Variation der Parameter.

2) Für verdünnte Gase gestattet die Berechnung der Transportkoeffizienten auf der Basis genauer Molekülmodelle, so etwa derjenigen nach Maxwell oder Lennard-Jones, und der Vergleich dieser Ergebnisse mit dem Experiment Rückschlüsse auf die tatsächliche molekulare Wechselwirkungsstruktur.

3) Die Anwendung der Boltzmann-Gleichung auf die metallische Leitfähigkeit liefert eine statistische Begründung des Ohmschen Gesetzes und der im Wiedemann-Franzschen Gesetz formulierten Proportionalität der Temperaturabhängigkeit von elektrischer und Wärmeleitfähigkeit.

4) In der Reaktorphysik werden Neutronentransportmechanismen meist auf der Grundlage der Boltzmann-Gleichung behandelt.

5) In der kinetischen Theorie inhomogener Plasmen führt die Anwendung der Boltzmann-Gleichung zur linearen Landau-Gleichung (Landau-Wlassow-Gleichung), die gleichzeitig einen Spezialfall der Fokker-Planck-Gleichung darstellt. [JS2]