Techniklexikon

Verteilungsfunktion

Mathematische Methoden und Computereinsatz,

1) Mathematik: wahrscheinlichkeitstheoretische Charakterisierung einer Zufallsgrösse. Die Verteilungsfunktion  der Zufallsgrösse  gibt die Wahrscheinlichkeit dafür an, dass die Zufallsgrösse einen Wert annimmt, der kleiner als  ist. Die Differenz  gibt die Wahrscheinlichkeit dafür an, dass  im Intervall  liegt. Aus der Definition der Verteilungsfunktion folgt, dass diese (schwach) monoton steigend ist, d.h. . Desweiteren gilt  und . Funktionen, die die Wahrscheinlichkeit dafür angeben, dass eine diskrete Zufallsgrösse  einen bestimmten Wert  aus einer abzählbaren Menge mit einer bestimmten Wahrscheinlichkeit  hat, heissen Wahrscheinlichkeitsfunktionen. Beispiele für Wahrscheinlichkeitsfunktionen diskreter Zufallsgrössen sind die Binomialverteilung, die hypergeometrische Verteilung und die Poisson-Verteilung. Im Falle stetiger Zufallsgrössen heissen die Wahrscheinlichkeitsfunktionen auch Dichte der Verteilung oder Verteilungsdichte. In diesem Falle gilt der Zusammenhang . Wichtigste Beispiele sind die Gleichverteilung und die Gauss-Verteilung.

2) Statistische Physik, Thermodynamik: synonymer Begriff für die Zustandssumme , wobei  die Wahrscheinlichkeit dafür angibt, dass sich ein thermodynamisches System mit Temperatur  im Energiezustand  befindet; aus  lassen sich dann alle thermodynamischen Funktionen berechnen.

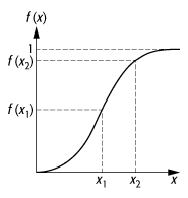
Verteilungsfunktion: Verteilungsfunktion einer stetigen Zufallsgrösse.