Techniklexikon

Streutheorie

Kernphysik, quantenmechanische Beschreibung der Streuung von Teilchen aneinander, wobei die Wechselwirkung durch ein Potential  charakterisiert wird. Im stationären Fall, bei dem ein zeitlich konstanter Strom von Teilchen mit Energie  auf das Streuzentrum hin läuft und ein ebensolcher, elastisch gestreuter Strahl weg läuft, wird die Streuung durch die stationäre Schrödinger-Gleichung  mit der Randbedingung, dass sich in grosser Entfernung vom Streuzentrum die Wellenfunktion als Überlagerung aus einfallender ebener Welle und auslaufender Kugelwelle darstellt, beschrieben:  für . Dabei ist  der Winkel zwischen der z-Achse und der Beobachtungsrichtung und  der Betrag des Wellenvektors. Die physikalische Information liegt in der durch das Potential bestimmten Streuamplitude , die sich nach Legendre-Polynomen entwickeln lässt,

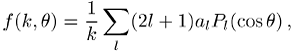
mit den Partialwellenamplituden ,  (für elastische Streuung ist ), die über  mit den S-Matrixelementen  vernüpft sind; die Streuphase  gibt die Phasenverschiebung der mit dem Drehimpuls l zur Streuung beitragenden Partialwelle an und kann bei schwachem Potential und grosser Einfallsenergie durch die Bornsche Näherung bestimmt werden. Die Bestimmung der Partialwellen, die an der Streuung beteiligt sind, bezeichnet man als Partialwellenanalyse; ihre Bedeutung liegt darin, dass besonders bei niedrigen Energien nur die niedrigsten Partialwellen beteiligt sind oder in der Nähe einer Resonanz zum Drehimpuls l_R nur dieser in der Summation berücksichtigt werden muss.

Der differentielle Wirkungsquerschnitt für elastische Streuung ist gegeben durch , der totale durch . Die Identität des elastischen Streuquerschnittes mit dem Imaginärteil der Vorwärtsstreuamplitude, , wird als optisches Theorem bezeichnet.

Für inelastische Streuung gilt , so dass  eine komplexe Zahl wird. Damit lautet der totale inelastische Streuquerschnitt

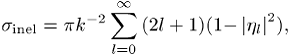
er hängt also nur vom Betrag von  ab. Jede inelastische Streuung hat auch einen elastischen Anteil mit

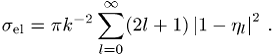
Für den gesamten totalen Wirkungsquerschnitt gilt das optische Theorem .

Eine wichtige Darstellung der S-Matrix als analytische Funktion liefern die holomorphen Jost-Funktionen ; auf diese Weise lassen sich auch gebundene Zustände und Resonanzen, die mit einer Halbwertszeit  wieder zerfallen, als komplexe Pole der S-Matrix beschreiben (Breit-Wigner-Formel). (Streuexperimente)