Techniklexikon

Jost-Funktion

spielt eine wesentliche Rolle in der Streutheorie in der Elementarteilchenphysik. Es seien f_l(±k,r) zwei linear unabhängigen Lösungen (»jost-solutions«) der radialen Schrödinger-Gleichung mit dem asymptotischen Verhalten

Mit der Jost-Funktion  lässt sich die Wellenfunktion f_l der partiellen Welle f mit Drehimpuls l darstellen als eine Linearkombination der beiden Lösungen f_l(±k,r):

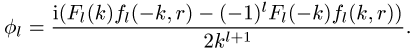
Die wichtigsten Eigenschaften der Jost-Funktion sind:

a) die komplexe Streuphase von F(k) ist mit der Phasenverschiebung identisch.

b) Die S-Matrix ist gegeben durch . Man kennt also die Streuamplitude, wenn man die Jost-Funktion zu sämtlichen Drehimpulsen l kennt.

c)  für gebundene Zustände mit , .

d) ,

d.h. F(k) ist eine holomorphe Funktion für . Diese Eigenschaften zeichnen die Jost-Funktion aus z.B. zur Berechnung von Wirkungsquerschnitten, aber vor allem in der inversen Streutheorie, wo versucht wird, aus Streudaten Wechselwirkungspotentiale zu rekonstruieren.