Techniklexikon

Sommerfeldsches Atommodell

Atom- und Molekülphysik, Erweiterung der Bohrschen Theorie des Atoms auf elliptische Bahnen (Ellipse). Analog zu den Planetenbahnen bewegt sich das Elektron nun auf Ellipsenbahnen um den Atomkern, der sich in einem der Brennpunkte befindet. Die Bewegung des Elektrons verfügt damit über zwei Freiheitsgrade. Sommerfeld stellte Quantisierungsbedingungen (Quantisierung) für die beiden konjugierten Impulse  und  auf:

Als Elektronenbahnen sind Ellipsen mit den grossen und kleinen Halbachsen

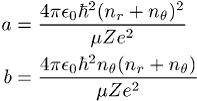
erlaubt, , da das Elektron auf einer Ellipse mit Exzentrizität null in den Kern stürzen müsste. Die Energie eines Elektrons auf diesen Ellipsenbahnen beträgt

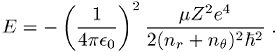
Vergleicht man diesen Ausdruck für die Gesamtenergie des Elektrons mit dem des Bohrschen Atommodells, so erkennt man, dass die Quantenzahlen mit der Hauptquantenzahl n des Bohrschen Modells gemäss  in Verbindung stehen. Mit n_r = 0 findet man auch die Bohrschen Kreisbahnen wieder. Üblicherweise charakterisiert man die Elektronenbahnen im Sommerfeldschen Atommodell mittels der Hauptquantenzahl n und der sog. azimuthalen Quantenzahl  (siehe Abb. 1). Wie im Bohrschen Atommodell ist die Energie des Elektrons nur von der Hauptquantenzahl n abhängig, nicht von der Exzentrizität der Elektronenbahn. Zur Erklärung der Feinstruktur der Spektrallinien des Wasserstoffatoms führte Sommerfeld eine relativistische Berechnung der Energie des Elektrons durch. Da die mittlere Geschwindigkeit des Elektrons von der Bahnform abhängt, kommen relativistische Effekte besonders bei den Ellipsenbahnen mit grosser Exzentrizität zum Tragen. Sommerfeld fand für die Elektronenenergie folgenden Ausdruck:

(a: Feinstrukturkonstante).

Die zugehörigen Elektronenbahnen waren nun keine geschlossenen Ellipsen mehr, sondern Rosettenbahnen (siehe Abb. 2).

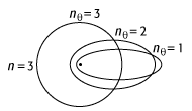
Sommerfeldsches Atommodell 1: Elliptische Elektronenbahnen nach dem Sommerfeldschen Atommodell für den Zustand n = 3 des Wasserstoffatoms.

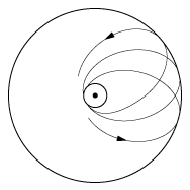
Sommerfeldsches Atommodell 2: Die Periheldrehung der relativistischen Ellipse führt zu einer Rosettenbahn.