Techniklexikon

konforme Feldtheorie

Zweig der Quantenfeldtheorie zur Beschreibung skaleninvarianter Systeme. Die entsprechende konforme Gruppe ist die Gruppe der winkeltreuen konformen Abbildungen der Minkowski-Raumzeit; sie enthält insbesondere die Poincaré-Gruppe und die Gruppe der globalen Skalierungen  als Untergruppe. Die physikalische Relevanz konformer Feldtheorien liegt zum einen in ihrer Anwendung auf kritische Modelle der Statistischen Mechanik (die durch Wick-Rotation in eine Quantenfeldtheorie überführt werden können) und zum anderen in ihrer engen Beziehung zur String-Theorie. Darüber hinaus gestattet die Lösung minimaler Modelle der statistischen Mechanik einen Zugang zu nichtstörungstheoretischen, exakten Wightman-Quantenfeldtheorien.

Die Beziehung zur String-Theorie ist dadurch gegeben, dass eine String-Wirkung

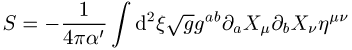
(a\' = 1 / 2 für offene und = 1 / 4 für geschlossene Strings; h^mn = (+, -, -, ...): Metrik der D-dimensionalen Raumzeit, g^ab: zweidimensionale Metrik der Oberfläche (Weltfläche), die vom String durch seine Bewegung in der Raumzeit aufgespannt wird) invariant unter Reparametrisierungen der Weltfläche

ist, falls

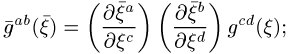
die Transformation von  hebt sich dann gerade gegen die Transformation des zweidimensionalen Integrationsmasses weg.

Eine Möglichkeit, die freie Theorie zu quantisieren, besteht in der Wahl der konformen Eichung g^ab = d^ab; die Lagrange-Dichte  lautet dann (mit z = s + it)

.

Die eichfixierte Wirkung ist zwar nicht mehr invariant unter lokalen Reparametrisierungen, aber immer noch global invariant unter konformen Transformationen

Der String transformiert dann wie

was zur Folge hat, dass der Energie-Impuls-Tensor

erhalten bleibt: ¶_aT^ab = 0. Seine Fourier-Koeffizienten L_n erzeugen die Virasoro-Algebra

Die physikalischen Zustände in der konformen Feldtheorie werden dementsprechend aus dem durch , (), und  definierten Vakuumzustand  mit Hilfe der Erzeugungsoperatoren L_-n gebildet. (String-Theorie)