Norm

Julian Schultheiss
Standard
Mathematische Methoden und
Computereinsatz, Länge oder Betrag eines Vektors. Gegeben sei ein Vektorraum ![]() über einem Körper
über einem Körper ![]() . Eine
Abbildung
. Eine
Abbildung ![]() heisst Norm auf
heisst Norm auf ![]() , falls für
alle
, falls für
alle ![]() und
und ![]() die Normaxiome
die Normaxiome
![]()
und die Dreiecksungleichung
![]()
gültig sind. Als Beispiel sei für beliebige reelle ![]() die
die ![]() -Norm eines
Vektors
-Norm eines
Vektors ![]() genannt:
genannt:
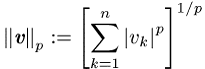
Der Spezialfall ![]() führt auf die Euklidische Norm, die mit der
anschaulichen geometrischen Länge eines Vektors übereinstimmt. Handelt es sich
bei
führt auf die Euklidische Norm, die mit der
anschaulichen geometrischen Länge eines Vektors übereinstimmt. Handelt es sich
bei ![]() um einen euklidischen bzw. unitären
Vektorraum, so gilt im Falle
um einen euklidischen bzw. unitären
Vektorraum, so gilt im Falle ![]() ferner
ferner
![]()
d.h. die Norm leitet sich aus dem Skalarprodukt ab. Die Wahl
einer geeigneten Norm in einem Vektorraum kann unter praktischen Erwägungen
erfolgen, denn für den Vektorraum ![]() lässt sich zeigen, dass alle Normen (nicht nur
die
lässt sich zeigen, dass alle Normen (nicht nur
die ![]() Normen) auf
dem
Normen) auf
dem ![]() äquivalent sind, d.h. für zwei beliebige
Normen
äquivalent sind, d.h. für zwei beliebige
Normen ![]() und
und ![]() auf dem
auf dem ![]() gibt es stets zwei positive Konstanten
gibt es stets zwei positive Konstanten ![]() und
und ![]() , so dass für
alle
, so dass für
alle ![]() gilt:
gilt:
![]()
Im erweiterten Sinne wird auch die Norm eines linearen
Operators bzw. einer Matrix definiert; es gelten sinngemäss die gleichen
Normaxiome. Eine Matrixnorm ![]() heisst verträglich mit einer Vektorraumnorm
heisst verträglich mit einer Vektorraumnorm ![]() , wenn für
alle Vektoren des Vektorraums
, wenn für
alle Vektoren des Vektorraums ![]() gilt. Beispiele für Matrixnormen sind die
Zeilensummennorm
gilt. Beispiele für Matrixnormen sind die
Zeilensummennorm
![]()
oder die mit der euklidischen Norm verträgliche Schur-Norm 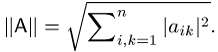
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.