Techniklexikon

Bloch-Gleichungen

1946 von F. Bloch aufgestelltes Gleichungssystem, das die zeitliche Entwicklung eines Spinsystems im Magnetfeld durch Präzession und Relaxation beschreibt:

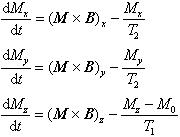
M ist die gesamte Kern- bzw. Elektronenmagnetisierung der Probe unter dem Einfluss des Magnetfeldes B. Bei magnetischen Resonanzexperimenten besteht B aus einem starken homogenen Magnetfeld B₀ in z-Richtung und einem senkrecht dazu in x-Richtung angelegten, hochfrequenten magnetischen Feld B_HF = 2B₁coswt. Dabei ist B = e_x2B₁coswt + e_zB₀, und B₁ << B₀. g ist das gyromagnetische Verhältnis der Atomkerne bzw. der Elektronen. T₁ ist die longitudinale oder Spin-Gitter-Relaxationszeit, d.h. die Zeitkonstante, mit der die Magnetisierung in z-Richtung ihrem Gleichgewichtswert M₀ = c₀ H zustrebt (B₀ = m H). T₂, die transversale oder Spin-Spin-Relaxationszeit, ist entsprechend die Zeitkonstante für die x- und y-Komponenten, wobei hier der Gleichgewichtswert null ist. Sie wird durch Spin-Spin-, Spin-Gitter-Wechselwirkungen und Inhomogenitäten des äusseren Magnetfeldes B₀ bestimmt.

Wichtige Spezialfälle der Bloch-Gleichungen sind die stationäre Lösung dM/dt = 0 bei den cw-Methoden (Dauerstrichlaser) und die freie Präzession in einem konstanten Magnetfeld entlang der z-Achse (typischer Fall bei den Puls-Verfahren) bei der magnetischen Resonanz.

Berücksichtigt man zusätzlich auch Effekte der Molekülbewegung (Diffusion und Fluss), so lautet die Gleichung für die x-Komponente folgendermassen (Bloch-Torrey-Gleichung):

( ist die Fliessgeschwindigkeit und D der Diffusionskoeffizient). Dabei muss berücksichtigt werden, dass der Diffusionskoeffizient D im allgemeinen Fall durch einen Tensor wiedergegeben wird.

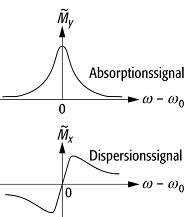
Bloch-Gleichungen